What Percent Of 80 Is 36
planetorganic
Nov 26, 2025 · 7 min read
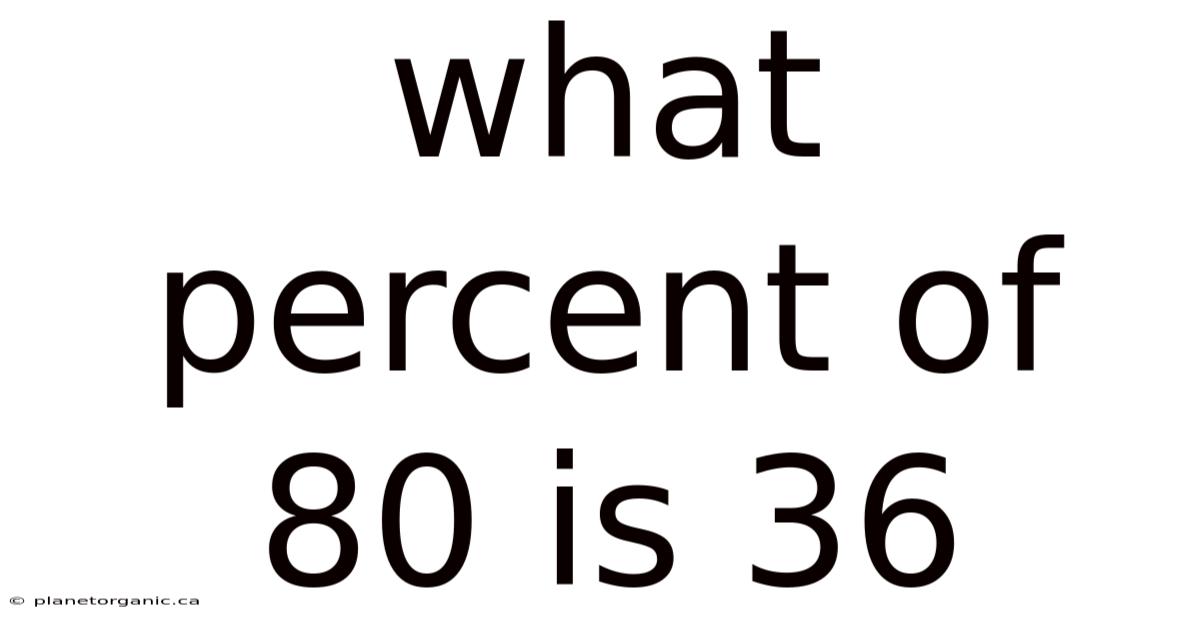
Table of Contents
Figuring out percentages is a fundamental skill with practical applications in everyday life, from calculating discounts at the store to understanding financial reports. In this article, we’ll break down the process of determining what percentage of 80 is 36. We'll explore the mathematical concepts involved, walk through the step-by-step calculations, and provide real-world examples to illustrate the concept. By the end, you'll be equipped with the knowledge and confidence to tackle similar percentage problems with ease.
Understanding Percentages
A percentage is a way to express a number as a fraction of 100. The word "percent" comes from the Latin "per centum," meaning "out of one hundred." Therefore, a percentage represents a ratio where the denominator is always 100. For example, 50% means 50 out of 100, which can be written as the fraction 50/100 or the decimal 0.50.
Percentages are used to describe proportions, ratios, or rates relative to a whole. They provide a standardized way to compare different quantities, making it easier to understand their relative sizes.
Basic Percentage Formula
The basic formula for calculating percentages is:
Percentage = (Part / Whole) × 100
Where:
- Part is the specific quantity you are interested in.
- Whole is the total quantity or the reference value.
This formula can be rearranged to solve for any of the variables, depending on the information you have and what you need to find.
Calculating "What Percent of 80 is 36?"
To determine what percentage of 80 is 36, we need to apply the percentage formula. In this case:
- Part = 36
- Whole = 80
Let's go through the calculation step-by-step.
Step 1: Set Up the Formula
Using the percentage formula, we can set up the equation as follows:
Percentage = (36 / 80) × 100
Step 2: Divide the Part by the Whole
Divide 36 by 80:
36 / 80 = 0.45
Step 3: Multiply by 100
Multiply the result by 100 to convert the decimal to a percentage:
- 45 × 100 = 45
Step 4: State the Answer
Therefore, 36 is 45% of 80.
Alternative Method: Using Proportions
Another way to solve percentage problems is by using proportions. A proportion is an equation stating that two ratios are equal. In this case, we can set up the proportion as follows:
36 / 80 = x / 100
Where:
- 36 is the part.
- 80 is the whole.
- x is the percentage we want to find.
Step 1: Cross-Multiply
Cross-multiply to solve for x:
36 × 100 = 80 × x
3600 = 80x
Step 2: Divide to Isolate x
Divide both sides by 80:
3600 / 80 = x
45 = x
Step 3: State the Answer
Therefore, 36 is 45% of 80.
Practical Examples and Applications
Understanding how to calculate percentages is crucial in many real-life situations. Here are a few examples:
1. Calculating Discounts
When shopping, you often encounter discounts expressed as percentages. Suppose an item originally priced at $80 is on sale for $36 off. To find the discount percentage:
- Part = $36 (the discount amount)
- Whole = $80 (the original price)
Percentage = (36 / 80) × 100 = 45%
The item is on sale for 45% off.
2. Determining Grades
In academic settings, percentages are used to calculate grades. Suppose you scored 36 points out of a possible 80 points on a test. To find your grade percentage:
- Part = 36 (your score)
- Whole = 80 (total possible score)
Percentage = (36 / 80) × 100 = 45%
Your grade on the test is 45%.
3. Analyzing Sales Data
Businesses use percentages to analyze sales data and track performance. Suppose a company sold 36 units of a product out of a total of 80 units available. To find the sales percentage:
- Part = 36 (units sold)
- Whole = 80 (total units available)
Percentage = (36 / 80) × 100 = 45%
The company sold 45% of the available units.
4. Understanding Survey Results
Percentages are commonly used in surveys to represent the proportion of respondents who selected a particular option. Suppose a survey of 80 people found that 36 of them prefer a certain brand. To find the percentage of people who prefer that brand:
- Part = 36 (number of people who prefer the brand)
- Whole = 80 (total number of respondents)
Percentage = (36 / 80) × 100 = 45%
45% of the respondents prefer the brand.
Common Mistakes to Avoid
While the percentage formula is straightforward, there are some common mistakes people make when calculating percentages:
-
Incorrectly Identifying the Part and Whole: Make sure you correctly identify which value is the part (the specific quantity you are interested in) and which is the whole (the total quantity or reference value).
-
Forgetting to Multiply by 100: After dividing the part by the whole, remember to multiply the result by 100 to convert the decimal to a percentage.
-
Misunderstanding the Question: Read the problem carefully to understand what percentage you are being asked to find. Sometimes the question might be phrased in a way that requires you to rearrange the percentage formula.
-
Rounding Errors: When dealing with decimals, be mindful of rounding errors. Round only at the final step to avoid accumulating errors in your calculations.
Advanced Percentage Problems
Once you have a solid understanding of the basic percentage formula, you can tackle more advanced percentage problems. Here are a few examples:
1. Percentage Increase and Decrease
Percentage increase and decrease are used to calculate the change in a quantity relative to its original value. The formulas are:
- Percentage Increase = ((New Value - Original Value) / Original Value) × 100
- Percentage Decrease = ((Original Value - New Value) / Original Value) × 100
For example, suppose a price increases from $80 to $100. To find the percentage increase:
- Original Value = $80
- New Value = $100
Percentage Increase = ((100 - 80) / 80) × 100 = (20 / 80) × 100 = 25%
The price increased by 25%.
2. Finding the Original Value
Sometimes you might need to find the original value given a percentage and a part. The formula is:
Original Value = Part / (Percentage / 100)
For example, suppose 36 is 45% of a number. To find the number:
- Part = 36
- Percentage = 45%
Original Value = 36 / (45 / 100) = 36 / 0.45 = 80
The original number is 80.
3. Compound Percentage Problems
Compound percentage problems involve multiple percentage changes applied sequentially. To solve these problems, you need to apply each percentage change one at a time.
For example, suppose a price increases by 20% and then decreases by 10%. If the original price is $80, to find the final price:
-
Increase by 20%:
- Increase Amount = 80 × 0.20 = $16
- Price after increase = 80 + 16 = $96
-
Decrease by 10%:
- Decrease Amount = 96 × 0.10 = $9.60
- Price after decrease = 96 - 9.60 = $86.40
The final price is $86.40.
Tips for Mastering Percentage Calculations
To become proficient in percentage calculations, consider the following tips:
-
Practice Regularly: The more you practice, the more comfortable you will become with the percentage formula and its applications.
-
Use Real-World Examples: Apply percentage calculations to real-world scenarios, such as calculating discounts while shopping or analyzing financial data.
-
Understand the Concepts: Focus on understanding the underlying concepts rather than memorizing formulas. This will help you apply percentages in a variety of situations.
-
Break Down Complex Problems: Break down complex problems into smaller, more manageable steps. This will make it easier to identify the part, whole, and percentage.
-
Check Your Answers: Always check your answers to ensure they are reasonable. If you are calculating a discount, make sure the discounted price is lower than the original price.
Conclusion
Calculating percentages is a fundamental skill with wide-ranging applications in everyday life. By understanding the basic percentage formula and practicing regularly, you can confidently solve percentage problems and make informed decisions. Whether you are calculating discounts, analyzing data, or understanding survey results, a solid grasp of percentages will serve you well. In the specific case of determining what percent of 80 is 36, we have shown that the answer is 45%. Keep practicing, and you'll master the art of percentage calculations in no time!
Latest Posts
Latest Posts
-
American History Judith Ortiz Cofer Summary
Nov 26, 2025
-
Nigeria Current Affairs Quiz Questions 2024
Nov 26, 2025
-
Objetivos Espesificos Y Generales Sobre Los Generos Liricos
Nov 26, 2025
-
How To Distinguish A Term Of Art In Legal Writing
Nov 26, 2025
-
Perks Of Being A Wallflower Script
Nov 26, 2025
Related Post
Thank you for visiting our website which covers about What Percent Of 80 Is 36 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.