What Percent Of 60 Is 57
planetorganic
Nov 13, 2025 · 8 min read
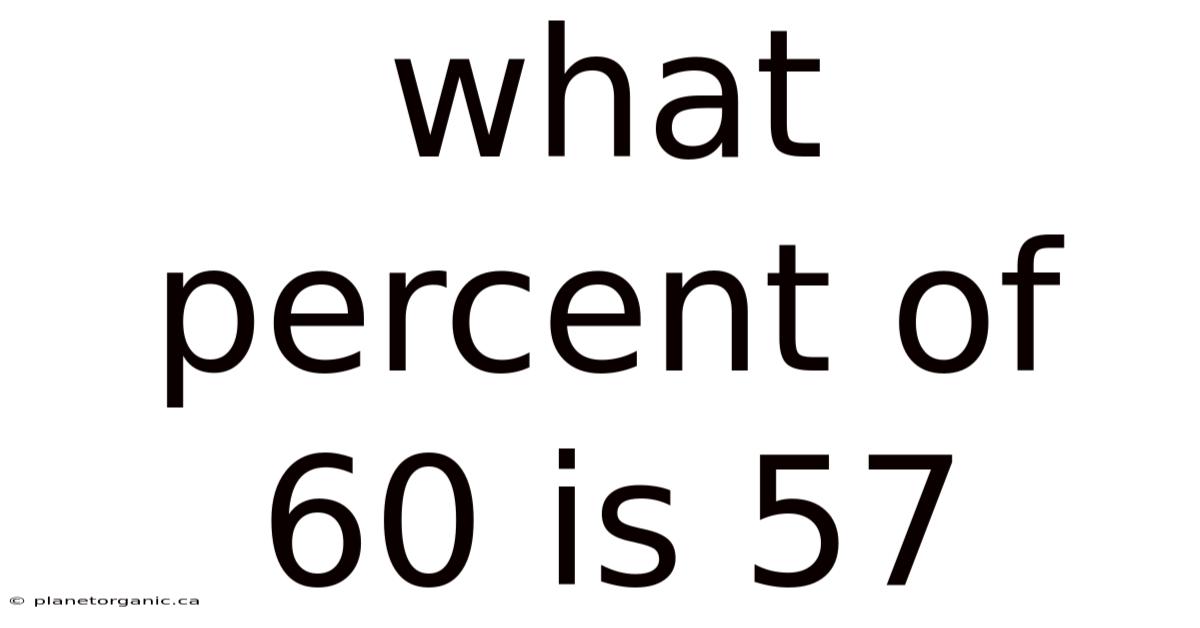
Table of Contents
Calculating percentages is a fundamental skill applicable in various real-world scenarios, from figuring out discounts to understanding statistical data. When we ask, "What percent of 60 is 57?", we're essentially trying to find out what proportion of 60 is represented by the number 57. This article will guide you through the step-by-step process of solving this type of percentage problem, provide numerous examples, and offer insights into why understanding percentages is crucial.
Understanding the Basics of Percentages
Before diving into the specifics of calculating what percentage of 60 is 57, let's establish a solid understanding of what percentages represent.
A percentage is a way of expressing a number as a fraction of 100. The term "percent" comes from the Latin "per centum," meaning "per hundred." In essence, when you say 50%, you mean 50 out of every 100. This makes percentages a standardized way to compare different proportions and rates.
The Percentage Formula
The basic formula to calculate a percentage is:
Percentage = (Part / Whole) × 100
Where:
- Part is the specific amount you're interested in.
- Whole is the total amount or the reference value.
Using this formula, we can tackle a wide range of percentage-related questions.
Step-by-Step Calculation: What Percent of 60 is 57?
To determine what percent of 60 is 57, we'll apply the percentage formula systematically.
Step 1: Identify the 'Part' and the 'Whole'
In our question:
- Part = 57 (This is the number we want to express as a percentage of 60.)
- Whole = 60 (This is the total amount or the reference value.)
Step 2: Apply the Percentage Formula
Now, we'll plug these values into our percentage formula:
Percentage = (57 / 60) × 100
Step 3: Perform the Division
First, divide the part (57) by the whole (60):
57 / 60 = 0.95
Step 4: Multiply by 100
Next, multiply the result by 100 to convert it into a percentage:
- 95 × 100 = 95%
Result
Therefore, 57 is 95% of 60.
Examples of Percentage Calculations
To solidify your understanding, let's go through some more examples similar to "what percent of 60 is 57."
Example 1: What Percent of 80 is 20?
- Identify the 'Part' and the 'Whole'
- Part = 20
- Whole = 80
- Apply the Percentage Formula
- Percentage = (20 / 80) × 100
- Perform the Division
- 20 / 80 = 0.25
- Multiply by 100
- 0.25 × 100 = 25%
Therefore, 20 is 25% of 80.
Example 2: What Percent of 150 is 45?
- Identify the 'Part' and the 'Whole'
- Part = 45
- Whole = 150
- Apply the Percentage Formula
- Percentage = (45 / 150) × 100
- Perform the Division
- 45 / 150 = 0.3
- Multiply by 100
- 0.3 × 100 = 30%
Therefore, 45 is 30% of 150.
Example 3: What Percent of 200 is 300?
This example is slightly different because the 'part' is larger than the 'whole,' resulting in a percentage greater than 100%.
- Identify the 'Part' and the 'Whole'
- Part = 300
- Whole = 200
- Apply the Percentage Formula
- Percentage = (300 / 200) × 100
- Perform the Division
- 300 / 200 = 1.5
- Multiply by 100
- 1.5 × 100 = 150%
Therefore, 300 is 150% of 200.
Example 4: Real-World Application - Sales Target
Suppose a salesperson has a target of selling 500 units a month. If they sell 400 units, what percentage of their target did they achieve?
- Identify the 'Part' and the 'Whole'
- Part = 400 (units sold)
- Whole = 500 (sales target)
- Apply the Percentage Formula
- Percentage = (400 / 500) × 100
- Perform the Division
- 400 / 500 = 0.8
- Multiply by 100
- 0.8 × 100 = 80%
The salesperson achieved 80% of their sales target.
Understanding Different Types of Percentage Problems
Percentage problems come in various forms. Here are some common types:
-
Finding a Percentage of a Number:
- Example: What is 20% of 50?
- Solution: (20/100) × 50 = 10
-
Finding What Percentage One Number is of Another:
- Example: What percent of 60 is 57? (As we've already covered)
-
Finding the Original Number Given a Percentage:
- Example: 10% of what number is 25?
- Solution: Let the number be x. (10/100) × x = 25 => x = 250
-
Percentage Increase:
- Example: If a price increases from $20 to $25, what is the percentage increase?
- Solution: ((New Value - Old Value) / Old Value) × 100 = ((25 - 20) / 20) × 100 = 25%
-
Percentage Decrease:
- Example: If a price decreases from $25 to $20, what is the percentage decrease?
- Solution: ((Old Value - New Value) / Old Value) × 100 = ((25 - 20) / 25) × 100 = 20%
Practical Applications of Percentage Calculations
Understanding how to calculate percentages is essential for numerous real-life situations:
1. Finance and Banking
- Interest Rates: Calculating interest on loans, savings accounts, and investments.
- Discounts and Sales: Determining the actual price after a discount.
- Financial Planning: Budgeting and tracking expenses as percentages of income.
2. Retail
- Discounts: Calculating sale prices and understanding markdowns.
- Markup: Determining the selling price based on cost and desired profit margin.
- Sales Tax: Calculating the total cost of a purchase including tax.
3. Health and Nutrition
- Nutrient Intake: Tracking macronutrient ratios (protein, carbs, fats) in a diet.
- Body Fat Percentage: Assessing health and fitness levels.
- Medication Dosage: Calculating the correct dosage based on body weight.
4. Education
- Grading: Calculating grades based on scores and assignments.
- Standardized Tests: Understanding percentile rankings.
- Statistics: Analyzing data and understanding distributions.
5. Business and Marketing
- Market Share: Determining a company's portion of the total market.
- Conversion Rates: Measuring the effectiveness of marketing campaigns.
- Profit Margins: Calculating the profitability of products or services.
6. Daily Life
- Tipping: Calculating appropriate tips at restaurants or for services.
- Cooking: Adjusting recipe quantities based on percentages.
- Home Improvement: Calculating material quantities for projects.
Common Mistakes to Avoid
While percentage calculations are straightforward, it’s easy to make errors if you’re not careful. Here are some common mistakes to avoid:
-
Confusing the 'Part' and the 'Whole':
- Ensure you correctly identify which number is the part (the specific amount) and which is the whole (the total amount).
-
Forgetting to Multiply by 100:
- Remember to multiply the result of the division by 100 to convert it into a percentage.
-
Incorrectly Applying Percentage Increase/Decrease Formulas:
- Use the correct formula: ((New Value - Old Value) / Old Value) × 100 for increase and ((Old Value - New Value) / Old Value) × 100 for decrease.
-
Rounding Errors:
- Be mindful of when and how you round numbers, as this can affect the final percentage.
-
Not Checking for Reasonableness:
- Always ask yourself if the calculated percentage makes sense in the context of the problem.
Advanced Tips and Tricks
Here are some advanced tips and tricks to enhance your understanding and speed up your percentage calculations:
1. Converting Percentages to Decimals
To quickly calculate percentages, convert them to decimals by dividing by 100. For example:
- 25% = 0.25
- 75% = 0.75
- 120% = 1.20
2. Using Benchmarks
Memorizing common percentage benchmarks can help you estimate percentages quickly. For example:
- 10% is one-tenth of the whole
- 25% is one-quarter of the whole
- 50% is one-half of the whole
- 75% is three-quarters of the whole
3. Mental Math Techniques
Practice mental math techniques to perform percentage calculations without a calculator. For example, to find 15% of 80:
- Calculate 10% of 80: 0.10 × 80 = 8
- Calculate 5% of 80 (half of 10%): 8 / 2 = 4
- Add the two results: 8 + 4 = 12
- Therefore, 15% of 80 is 12.
4. Cross-Multiplication
Cross-multiplication can be useful for solving percentage problems where you need to find an unknown value. For example:
If 30% of x is 45, find x.
- Set up the proportion: 30/100 = 45/x
- Cross-multiply: 30x = 4500
- Solve for x: x = 4500 / 30 = 150
5. Using Percentage Calculators
When dealing with complex calculations or needing precise results, use online percentage calculators or spreadsheet software. These tools can save time and reduce the risk of errors.
The Role of Percentages in Statistics
Percentages play a crucial role in statistics, providing a standardized way to interpret and compare data. Here are some key applications:
1. Descriptive Statistics
Percentages are used to describe the characteristics of a dataset. For example, in a survey, you might report the percentage of respondents who agree with a particular statement.
2. Inferential Statistics
Percentages are used to make inferences about a population based on a sample. For example, you might use the percentage of voters in a sample who support a candidate to estimate the percentage of all voters who support the candidate.
3. Probability
Percentages are used to express probabilities. For example, if there's a 20% chance of rain, it means that in similar conditions, it will rain 20 out of 100 times.
4. Hypothesis Testing
Percentages are used to test hypotheses. For example, you might compare the percentage of patients who recover with a new treatment to the percentage who recover with a standard treatment to see if the new treatment is more effective.
5. Data Visualization
Percentages are used in charts and graphs to visually represent data. For example, pie charts often use percentages to show the proportion of different categories.
Conclusion
Understanding how to calculate percentages is a fundamental skill with wide-ranging applications. Whether you're figuring out discounts, analyzing data, or managing your finances, percentages are an essential tool. By mastering the basic formula, practicing with examples, and avoiding common mistakes, you can confidently tackle any percentage-related problem. So, remember: to find what percent of 60 is 57, simply divide 57 by 60 and multiply by 100, resulting in 95%. Keep practicing, and you'll become a percentage pro in no time!
Latest Posts
Latest Posts
-
This Region Of Africa Is Home To The Orange River
Nov 13, 2025
-
Acceleration Due To Gravity Lab Report
Nov 13, 2025
-
America The Story Of Us Cities Answers
Nov 13, 2025
-
3 4 11 Practice Spoken Assignment The Great Outdoors
Nov 13, 2025
-
A Rational Decision Maker Takes An Action Only If The
Nov 13, 2025
Related Post
Thank you for visiting our website which covers about What Percent Of 60 Is 57 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.