What Percent Of 40 Is 38
planetorganic
Nov 14, 2025 · 8 min read
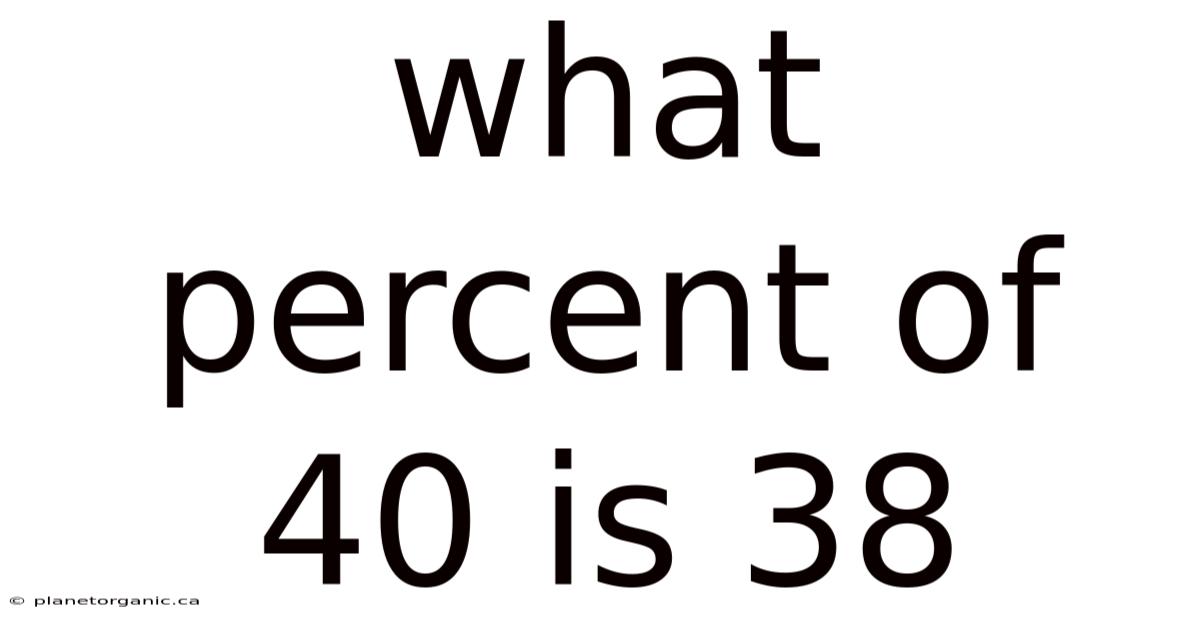
Table of Contents
The question "What percent of 40 is 38?" is a common type of percentage problem that appears in various contexts, from academic settings to everyday financial calculations. Understanding how to solve these types of problems is crucial for making informed decisions and accurately interpreting data. This article will provide a detailed explanation of how to calculate what percentage one number is of another, along with practical examples and a comprehensive guide to mastering percentage problems.
Understanding Percentage Basics
Percentage is a way of expressing a number as a fraction of 100. It is denoted by the percent sign "%." When we say "X percent," we mean X out of 100, which can be written as X/100. Percentages are used to represent proportions, ratios, or changes in values in a standardized format, making it easier to compare different quantities.
Key Concepts
Before diving into the calculation, it’s essential to understand a few key concepts:
- Base Number: The total or whole amount to which another number is compared. In the question "What percent of 40 is 38?", 40 is the base number.
- Percentage: The rate per hundred. It’s what we’re trying to find.
- Amount: The part of the base number that we are interested in. In this case, it's 38.
The Formula
To find what percentage a number (amount) is of another number (base), you can use the following formula:
Percentage = (Amount / Base) * 100
This formula essentially calculates the ratio of the amount to the base and then converts it to a percentage by multiplying by 100.
Step-by-Step Calculation: What Percent of 40 is 38?
Let's apply the formula to solve the problem: "What percent of 40 is 38?"
- Identify the Base and Amount:
- Base = 40
- Amount = 38
- Apply the Formula:
- Percentage = (38 / 40) * 100
- Perform the Division:
- 38 / 40 = 0.95
- Multiply by 100:
-
- 95 * 100 = 95
-
- Result:
- Therefore, 38 is 95% of 40.
Detailed Explanation
- Division: Dividing 38 by 40 gives you the decimal value representing the proportion of 38 relative to 40. In this case, 0.95 indicates that 38 is 0.95 times the value of 40.
- Multiplication by 100: Multiplying the decimal by 100 converts it into a percentage. This is because percentages are expressed as a fraction of 100. So, 0.95 becomes 95%, meaning 38 is 95 parts out of 100 of 40.
Practical Examples of Percentage Calculations
To further illustrate the concept, let’s explore some practical examples.
Example 1: Calculating a Discount
Suppose a store offers a discount on a product. The original price of the product is $50, and the discounted price is $40. What is the percentage discount?
- Find the Discount Amount:
- Discount Amount = Original Price - Discounted Price
- Discount Amount = $50 - $40 = $10
- Identify the Base and Amount:
- Base (Original Price) = $50
- Amount (Discount Amount) = $10
- Apply the Formula:
- Percentage Discount = (Discount Amount / Original Price) * 100
- Percentage Discount = ($10 / $50) * 100
- Perform the Division:
- $10 / $50 = 0.2
- Multiply by 100:
-
- 2 * 100 = 20
-
- Result:
- The percentage discount is 20%.
Example 2: Calculating a Test Score
A student scored 75 out of 100 on a test. What percentage did the student score?
- Identify the Base and Amount:
- Base (Total Score) = 100
- Amount (Student's Score) = 75
- Apply the Formula:
- Percentage Score = (Student's Score / Total Score) * 100
- Percentage Score = (75 / 100) * 100
- Perform the Division:
- 75 / 100 = 0.75
- Multiply by 100:
-
- 75 * 100 = 75
-
- Result:
- The student scored 75%.
Example 3: Calculating Percentage Increase
A company's revenue increased from $200,000 to $250,000 in a year. What is the percentage increase in revenue?
- Find the Increase Amount:
- Increase Amount = New Revenue - Old Revenue
- Increase Amount = $250,000 - $200,000 = $50,000
- Identify the Base and Amount:
- Base (Original Revenue) = $200,000
- Amount (Increase Amount) = $50,000
- Apply the Formula:
- Percentage Increase = (Increase Amount / Original Revenue) * 100
- Percentage Increase = ($50,000 / $200,000) * 100
- Perform the Division:
- $50,000 / $200,000 = 0.25
- Multiply by 100:
-
- 25 * 100 = 25
-
- Result:
- The percentage increase in revenue is 25%.
Common Mistakes to Avoid
While the formula for calculating percentages is straightforward, there are common mistakes that people make. Avoiding these pitfalls can ensure accurate calculations.
- Incorrectly Identifying the Base:
- One of the most common errors is misidentifying the base number. The base is the total or whole amount to which you are comparing the other number. Make sure you correctly identify which number represents the total.
- Forgetting to Multiply by 100:
- After dividing the amount by the base, you must multiply the result by 100 to express it as a percentage. Failing to do so will give you a decimal, not a percentage.
- Mixing Up the Amount and Base:
- Ensure that you place the correct numbers in the formula. The amount is the part you are interested in, while the base is the total.
- Rounding Errors:
- When dealing with decimals, rounding errors can occur. It’s best to keep as many decimal places as possible during the calculation and round only at the final step.
- Misinterpreting Percentage Change:
- When calculating percentage increase or decrease, make sure you use the original value as the base. Using the new value as the base will lead to an incorrect percentage change.
Advanced Percentage Problems
Beyond basic calculations, percentages can be used in more complex problems involving multiple steps or variables.
Compound Percentage Change
Calculating compound percentage changes involves applying successive percentage increases or decreases. For example, if a price increases by 10% one year and then decreases by 5% the next year, the overall percentage change is not simply 10% - 5% = 5%.
To calculate the compound percentage change:
- Initial Value: Assume an initial value (e.g., 100).
- Apply the First Change:
- If the value increases by 10%, the new value is 100 + (10% of 100) = 110.
- Apply the Second Change:
- If the value decreases by 5%, the new value is 110 - (5% of 110) = 110 - 5.5 = 104.5.
- Calculate the Overall Change:
- Overall Change = Final Value - Initial Value
- Overall Change = 104.5 - 100 = 4.5
- Express as a Percentage:
- Overall Percentage Change = (Overall Change / Initial Value) * 100
- Overall Percentage Change = (4.5 / 100) * 100 = 4.5%
Reverse Percentage Problems
Reverse percentage problems involve finding the original value when you know the final value and the percentage change. For example, if a price is $60 after a 20% discount, what was the original price?
- Understand the Relationship:
- The final price is 80% of the original price (since it’s a 20% discount).
- Set Up the Equation:
-
- 8 * Original Price = $60
-
- Solve for the Original Price:
- Original Price = $60 / 0.8
- Original Price = $75
Percentage Mixtures
Percentage mixtures involve combining different quantities with different percentages to find the overall percentage. For example, if you mix 100 grams of a 20% solution with 200 grams of a 30% solution, what is the percentage of the resulting solution?
- Calculate the Amount of Solute in Each Solution:
- Amount of Solute in 20% Solution = 20% of 100 grams = 0.2 * 100 = 20 grams
- Amount of Solute in 30% Solution = 30% of 200 grams = 0.3 * 200 = 60 grams
- Calculate the Total Amount of Solute:
- Total Amount of Solute = 20 grams + 60 grams = 80 grams
- Calculate the Total Weight of the Mixture:
- Total Weight of Mixture = 100 grams + 200 grams = 300 grams
- Calculate the Percentage of the Resulting Solution:
- Percentage = (Total Amount of Solute / Total Weight of Mixture) * 100
- Percentage = (80 / 300) * 100
- Percentage = 26.67% (approximately)
Real-World Applications of Percentage Calculations
Percentage calculations are essential in many real-world scenarios. Here are some examples:
- Finance: Calculating interest rates, investment returns, loan payments, and taxes.
- Retail: Determining discounts, markups, sales tax, and profit margins.
- Statistics: Analyzing data, calculating probabilities, and interpreting survey results.
- Health: Monitoring health indicators, calculating medication dosages, and understanding medical research.
- Education: Grading tests, calculating grade point averages, and analyzing student performance.
- Business: Analyzing market trends, forecasting sales, and managing budgets.
Tips for Mastering Percentage Problems
Mastering percentage problems requires practice and a solid understanding of the underlying concepts. Here are some tips to help you improve your skills:
- Practice Regularly: The more you practice, the more comfortable you will become with percentage calculations. Work through a variety of problems to build your confidence.
- Understand the Concepts: Make sure you understand the basic concepts of percentages, including the definition of percentage, base, and amount.
- Use Visual Aids: Visual aids, such as diagrams and charts, can help you understand and solve percentage problems.
- Check Your Work: Always check your work to ensure that you have correctly identified the base and amount and that you have performed the calculations accurately.
- Break Down Complex Problems: Break down complex problems into smaller, more manageable steps. This will make it easier to identify the relevant information and perform the calculations correctly.
- Use Online Resources: There are many online resources available to help you learn and practice percentage calculations, including tutorials, practice problems, and calculators.
Conclusion
Understanding how to calculate percentages is a fundamental skill that is essential for success in many areas of life. Whether you are calculating discounts at the store, analyzing financial data, or interpreting survey results, percentages play a crucial role in decision-making and problem-solving. By mastering the basic concepts, avoiding common mistakes, and practicing regularly, you can become proficient in percentage calculations and confidently apply them to real-world situations. In the case of "What percent of 40 is 38?", the answer is 95%, a testament to the precision and utility of percentage calculations in our daily lives.
Latest Posts
Latest Posts
-
How Many Waves Are There In This Wave Train
Nov 14, 2025
-
Unit 9 Progress Check Mcq Ap Chem
Nov 14, 2025
-
The Biggest Difference Between Mores And Folkways Is That
Nov 14, 2025
-
Book Of Wisdom Volume 2 Pdf Free Download
Nov 14, 2025
-
In A Unified Command Members Representing Multiple Jurisdictions And Agencies
Nov 14, 2025
Related Post
Thank you for visiting our website which covers about What Percent Of 40 Is 38 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.