What Percent Of 16 Is 4
planetorganic
Nov 27, 2025 · 8 min read
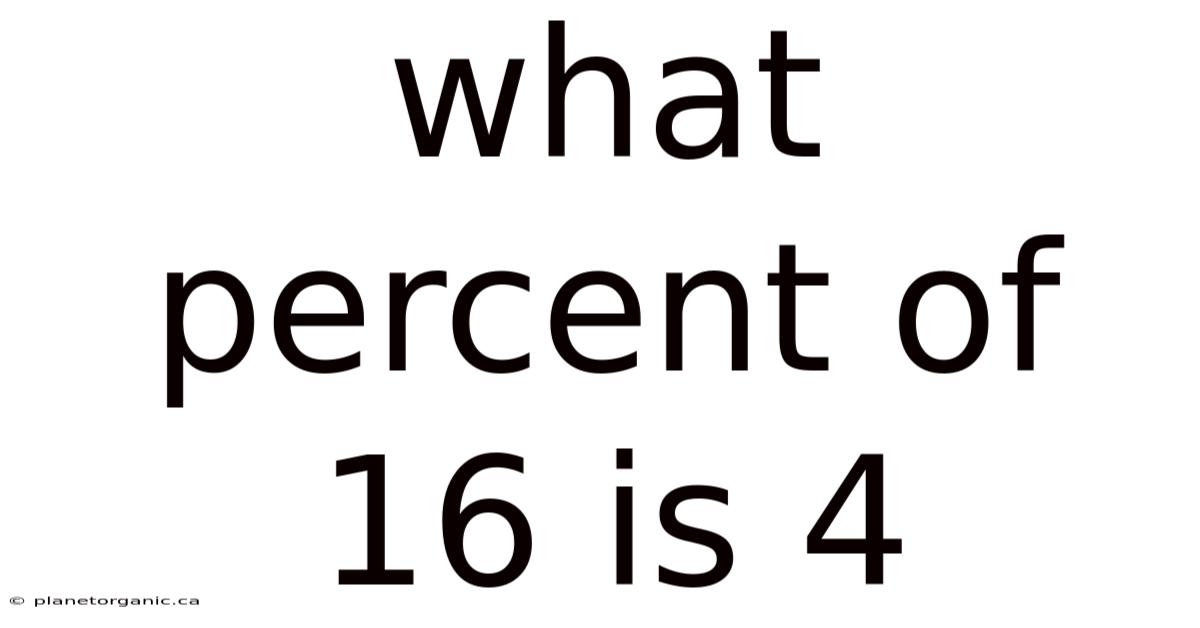
Table of Contents
Unveiling the Percentage: Determining What Percent of 16 is 4
Understanding percentages is a crucial skill in various aspects of life, from calculating discounts to analyzing data. This article dives into the process of finding what percentage of 16 is represented by the number 4. We'll explore the fundamental concepts, break down the calculation step-by-step, and provide examples to solidify your understanding. By the end of this guide, you'll be confident in tackling similar percentage problems and applying this knowledge to real-world scenarios.
Understanding the Basics: Percentage Explained
At its core, a percentage represents a portion of a whole, expressed as a fraction of 100. The word "percent" itself comes from the Latin per centum, meaning "out of one hundred." Essentially, a percentage provides a standardized way to compare different ratios and proportions.
Think of a pie divided into 100 slices. Each slice represents 1%. If you have 25 slices, you have 25% of the pie. Similarly, if you have 50 slices, you have 50%, which is also half of the pie.
Percentages are denoted by the symbol "%". For example, 25% is read as "twenty-five percent." They can also be expressed as decimals or fractions:
- 25% = 0.25 = 1/4
The ability to convert between percentages, decimals, and fractions is fundamental to understanding and working with percentage problems.
Setting Up the Problem: Identifying the Components
Before we can calculate what percent of 16 is 4, we need to identify the key components of the problem:
- The Base: This is the whole or the total amount that we are comparing to. In our case, the base is 16. We are trying to determine what percentage of 16 is represented by another number.
- The Part: This is the portion of the base that we are interested in. Here, the part is 4. We want to know what percentage of 16 is equal to 4.
- The Percentage: This is the unknown value that we are trying to find. It represents the proportion of the part relative to the base, expressed as a percentage.
In essence, we are looking for the value of "x" in the following statement:
- x% of 16 = 4
The Formula: Connecting the Pieces
The relationship between the base, the part, and the percentage can be expressed using the following formula:
- Percentage = (Part / Base) * 100
This formula provides a straightforward method for calculating the percentage when the part and the base are known.
Let's break down why this formula works:
- Part / Base: This calculates the fraction representing the proportion of the part relative to the base. For example, if the part is half of the base, this fraction will be 0.5.
- Multiplying by 100: Multiplying the fraction by 100 converts it into a percentage. This is because percentages are expressed as a fraction out of 100. So, 0.5 multiplied by 100 becomes 50%, indicating that the part represents 50% of the base.
Step-by-Step Calculation: Finding the Solution
Now that we understand the formula and the components, we can apply it to our problem: What percent of 16 is 4?
-
Identify the Part and the Base:
- Part = 4
- Base = 16
-
Apply the Formula:
- Percentage = (Part / Base) * 100
- Percentage = (4 / 16) * 100
-
Simplify the Fraction:
- 4 / 16 can be simplified to 1 / 4
-
Calculate the Decimal Equivalent:
- 1 / 4 = 0.25
-
Multiply by 100:
- 0.25 * 100 = 25
Therefore, 4 is 25% of 16.
Verifying the Answer: Ensuring Accuracy
It's always a good practice to verify your answer to ensure accuracy. We can do this by calculating 25% of 16 and confirming that it equals 4.
To calculate 25% of 16, we can use the following formula:
- Value = Percentage * Base
- Value = (25 / 100) * 16
- Value = 0.25 * 16
- Value = 4
Since our calculation results in 4, which is the part we started with, we can confidently confirm that our answer is correct. 4 is indeed 25% of 16.
Real-World Applications: Putting Percentages to Work
Understanding how to calculate percentages is not just a theoretical exercise; it has numerous practical applications in our daily lives. Here are a few examples:
- Discounts and Sales: When shopping, you often encounter discounts expressed as percentages. For example, a 20% discount on a $50 item means you save 20% of $50, which is $10. The final price you pay is $50 - $10 = $40.
- Calculating Tips: When dining at a restaurant, it's customary to leave a tip for the server. A common tip amount is 15% or 20% of the bill. Knowing how to calculate percentages allows you to quickly determine the appropriate tip amount.
- Analyzing Data: Percentages are frequently used in data analysis to represent proportions and trends. For instance, you might see statistics like "70% of customers prefer product A over product B" or "The unemployment rate has decreased by 2%."
- Financial Planning: Percentages are crucial for managing your finances. You might calculate the percentage of your income that goes towards rent, savings, or debt repayment. Understanding interest rates, which are expressed as percentages, is also essential for making informed financial decisions.
- Academic Performance: Your grades are often expressed as percentages. A score of 85% on an exam means you answered 85 out of 100 questions correctly. Percentages help you track your progress and compare your performance across different subjects.
These are just a few examples, and the applications of percentages are virtually limitless. Mastering this fundamental concept will undoubtedly benefit you in various aspects of your personal and professional life.
Exploring Variations: Different Types of Percentage Problems
While we've focused on finding the percentage when the part and the base are known, there are other types of percentage problems you might encounter. Here's a brief overview:
-
Finding the Part: In this type of problem, you are given the percentage and the base, and you need to find the part. For example, "What is 30% of 80?" To solve this, you would use the formula: Part = (Percentage / 100) * Base. So, Part = (30 / 100) * 80 = 24.
-
Finding the Base: Here, you are given the percentage and the part, and you need to find the base. For example, "15 is 25% of what number?" To solve this, you would rearrange the formula: Base = Part / (Percentage / 100). So, Base = 15 / (25 / 100) = 60.
Being able to recognize and solve these different types of percentage problems will enhance your overall understanding and problem-solving abilities.
Common Mistakes to Avoid: Ensuring Accuracy
When working with percentages, it's easy to make mistakes if you're not careful. Here are some common pitfalls to avoid:
-
Misidentifying the Base: One of the most common errors is incorrectly identifying the base. Always pay close attention to the wording of the problem to determine which value represents the whole or the total amount.
-
Forgetting to Convert to Decimal or Fraction: When using the formulas, remember to convert the percentage to a decimal or fraction before performing the calculations. For example, 25% should be converted to 0.25 or 1/4.
-
Incorrectly Applying the Formula: Make sure you are using the correct formula for the type of problem you are solving. As we discussed earlier, different types of percentage problems require different formulas.
-
Rounding Errors: Be mindful of rounding errors, especially when dealing with decimals. Round your answers to an appropriate number of decimal places based on the context of the problem.
-
Failing to Verify Your Answer: As we emphasized earlier, always verify your answer to ensure accuracy. This simple step can help you catch errors and build confidence in your solution.
By being aware of these common mistakes and taking steps to avoid them, you can significantly improve your accuracy and proficiency in working with percentages.
Advanced Techniques: Percentage Change and Growth
Beyond the basic calculations, there are more advanced concepts related to percentages, such as percentage change and growth. These concepts are particularly relevant in fields like finance, economics, and statistics.
-
Percentage Change: This measures the relative change in a value over time. It is calculated using the following formula:
- Percentage Change = [(New Value - Old Value) / Old Value] * 100
For example, if a stock price increases from $50 to $60, the percentage change is:
- Percentage Change = [($60 - $50) / $50] * 100 = 20%
A positive percentage change indicates an increase, while a negative percentage change indicates a decrease.
-
Percentage Growth: This is a specific type of percentage change that measures the increase in a value over time. It is calculated using the same formula as percentage change, but it is typically used in the context of growth rates, such as population growth or economic growth.
Understanding percentage change and growth allows you to analyze trends, compare performance, and make informed decisions in various contexts.
Practice Problems: Testing Your Knowledge
To solidify your understanding of percentages, here are some practice problems for you to try:
- What percent of 50 is 10?
- What is 15% of 120?
- 20 is 40% of what number?
- A store is offering a 30% discount on a shirt that originally costs $40. What is the sale price of the shirt?
- A company's revenue increased from $1 million to $1.2 million. What is the percentage change in revenue?
Work through these problems, applying the formulas and techniques we've discussed. Check your answers to ensure you've grasped the concepts correctly.
Conclusion: Mastering the Art of Percentages
Calculating what percent of 16 is 4, and more generally, mastering the concept of percentages, is an essential skill that empowers you in numerous aspects of life. From everyday tasks like calculating discounts and tips to more complex applications in finance and data analysis, a solid understanding of percentages is invaluable.
By understanding the basic principles, applying the correct formulas, and avoiding common mistakes, you can confidently tackle percentage problems and leverage this knowledge to make informed decisions. So, continue practicing, exploring advanced concepts, and applying your understanding to real-world scenarios. With dedication and effort, you can master the art of percentages and unlock its full potential. The answer, as we've determined, is 25%. Now go forth and conquer the world of percentages!
Latest Posts
Latest Posts
-
What Do The Two Ds In Cheddar Stand For
Nov 27, 2025
-
Who Decides What Problems Should Be Addressed Through Fiscal Policy
Nov 27, 2025
-
Rn Maternal Newborn Online Practice 2019 A With Ngn
Nov 27, 2025
-
Which Of The Following Is Not A Boolean Operator
Nov 27, 2025
-
Solicitud De Permiso Por Salud Word
Nov 27, 2025
Related Post
Thank you for visiting our website which covers about What Percent Of 16 Is 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.