What Percent Of 126 Is 22
planetorganic
Nov 20, 2025 · 8 min read
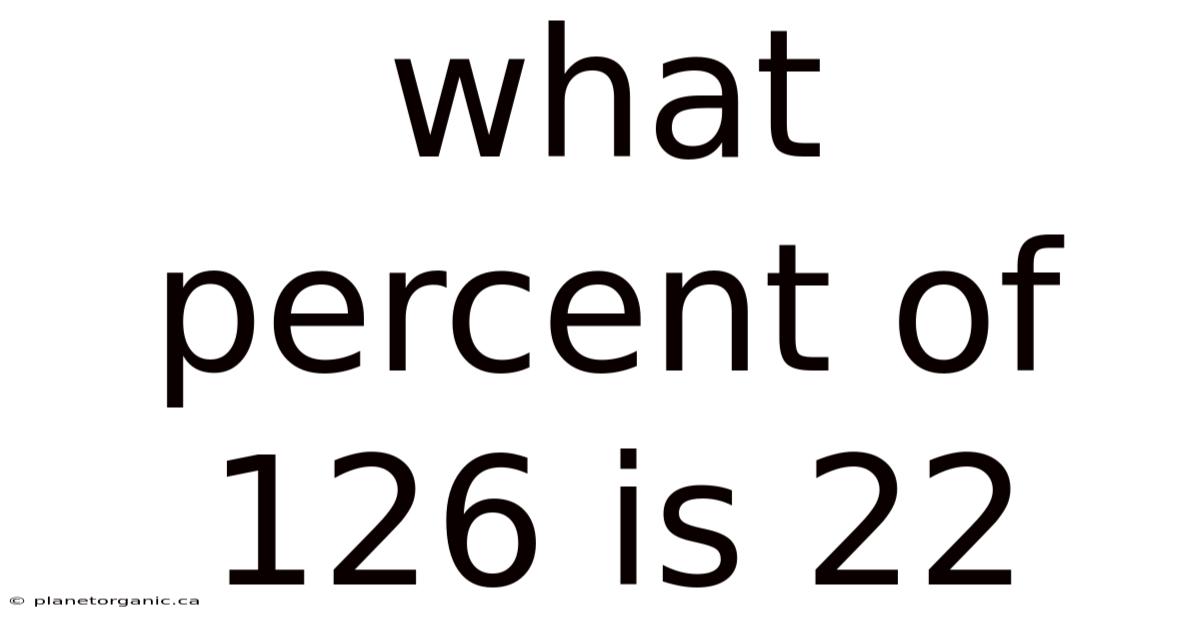
Table of Contents
Determining the percentage that one number represents of another is a fundamental mathematical skill with applications spanning personal finance, data analysis, and academic pursuits. Understanding how to calculate percentages accurately allows for meaningful comparisons and informed decision-making. In this detailed exploration, we'll break down the process of finding what percent of 126 is 22, covering the underlying concepts, step-by-step calculations, practical examples, and common pitfalls to avoid.
Understanding the Basics of Percentages
At its core, a percentage is a way of expressing a number as a fraction of 100. The word "percent" comes from the Latin "per centum," meaning "out of one hundred." Percentages are denoted by the symbol %, and they provide a standardized way to compare different quantities.
To express a number as a percentage, you divide it by the total quantity and then multiply the result by 100. The formula for calculating a percentage is:
Percentage = (Part / Whole) * 100
Where:
- Part is the value you want to express as a percentage of the whole.
- Whole is the total quantity or the reference value.
For example, if you scored 80 out of 100 on a test, your percentage score would be (80 / 100) * 100 = 80%.
Calculating What Percent of 126 is 22
Now, let's apply this concept to the specific question: What percent of 126 is 22? In this case, 22 is the "part" and 126 is the "whole." Using the formula, we can calculate the percentage as follows:
Percentage = (22 / 126) * 100
Step 1: Divide the Part by the Whole
First, divide 22 by 126:
22 / 126 ≈ 0.1746
Step 2: Multiply by 100
Next, multiply the result by 100 to express it as a percentage:
- 1746 * 100 = 17.46%
Therefore, 22 is approximately 17.46% of 126.
Step-by-Step Guide with Examples
To further illustrate the process, let's consider a few additional examples:
Example 1: Finding What Percent of 50 is 10
- Part = 10
- Whole = 50
- Percentage = (10 / 50) * 100 = 20%
So, 10 is 20% of 50.
Example 2: Finding What Percent of 200 is 35
- Part = 35
- Whole = 200
- Percentage = (35 / 200) * 100 = 17.5%
Thus, 35 is 17.5% of 200.
Example 3: Finding What Percent of 300 is 75
- Part = 75
- Whole = 300
- Percentage = (75 / 300) * 100 = 25%
Hence, 75 is 25% of 300.
Practical Applications of Percentage Calculations
Understanding percentage calculations is crucial in various real-world scenarios. Here are some common applications:
- Finance: Calculating interest rates, discounts, and investment returns.
- Retail: Determining sale prices, markups, and profit margins.
- Statistics: Analyzing data, interpreting survey results, and presenting findings.
- Education: Evaluating student performance, grading assignments, and comparing scores.
- Health: Monitoring changes in weight, tracking medication dosages, and assessing health risks.
Finance:
Consider a scenario where you want to buy a laptop that originally costs $1200, but it's on sale for $900. To find the percentage discount, you would calculate:
- Discount amount = $1200 - $900 = $300
- Percentage discount = ($300 / $1200) * 100 = 25%
Therefore, the laptop is on sale for a 25% discount.
Retail:
A store buys a product for $50 and wants to sell it with a 30% markup. To find the selling price, they would calculate:
- Markup amount = $50 * 0.30 = $15
- Selling price = $50 + $15 = $65
Thus, the store will sell the product for $65.
Statistics:
In a survey of 500 people, 350 prefer coffee over tea. To find the percentage of people who prefer coffee, you would calculate:
- Percentage = (350 / 500) * 100 = 70%
Hence, 70% of the people surveyed prefer coffee.
Common Mistakes to Avoid
While calculating percentages is straightforward, there are several common mistakes to watch out for:
- Incorrectly Identifying the Part and Whole: Ensure you correctly identify which number is the part and which is the whole. Confusing them will lead to an incorrect percentage.
- Forgetting to Multiply by 100: After dividing the part by the whole, remember to multiply the result by 100 to express it as a percentage.
- Rounding Errors: Be mindful of rounding errors, especially when dealing with decimal numbers. Rounding too early in the calculation can lead to significant inaccuracies.
- Misinterpreting the Question: Always read the question carefully to understand what percentage is being asked for.
Advanced Percentage Calculations
Beyond the basic calculations, there are more advanced percentage concepts to explore:
- Percentage Increase and Decrease: Calculating the percentage change between two values.
- Percentage Points: The difference between two percentages.
- Weighted Averages: Calculating averages where different values have different weights or importance.
Percentage Increase and Decrease:
To calculate the percentage increase or decrease between two values, use the following formulas:
- Percentage Increase = ((New Value - Old Value) / Old Value) * 100
- Percentage Decrease = ((Old Value - New Value) / Old Value) * 100
For example, if a stock's price increases from $50 to $60, the percentage increase is:
- Percentage Increase = (($60 - $50) / $50) * 100 = 20%
If the price then decreases from $60 to $45, the percentage decrease is:
- Percentage Decrease = (($60 - $45) / $60) * 100 = 25%
Percentage Points:
Percentage points are used to describe the difference between two percentages. For example, if a candidate's approval rating increases from 40% to 45%, the increase is 5 percentage points, not 5%.
Weighted Averages:
Weighted averages are used when different values have different weights or importance. For example, in a course, assignments might be worth 20% of the final grade, quizzes 30%, and the final exam 50%. To calculate the weighted average, you would multiply each grade by its weight and then sum the results.
Using Technology to Simplify Percentage Calculations
In today's digital age, numerous tools can simplify percentage calculations:
- Calculators: Basic calculators can perform simple percentage calculations quickly and accurately.
- Spreadsheet Software: Programs like Microsoft Excel and Google Sheets have built-in functions for calculating percentages and performing more complex statistical analyses.
- Online Percentage Calculators: Numerous websites offer free percentage calculators that can handle various types of percentage calculations.
- Mobile Apps: Many mobile apps are available for calculating percentages on the go.
Practical Examples Revisited
Let's revisit some practical examples, applying the concepts we've discussed:
Example 1: Budgeting
Suppose you have a monthly income of $3000 and you want to allocate 15% of it to savings. How much money should you save each month?
- Savings amount = $3000 * 0.15 = $450
Therefore, you should save $450 each month.
Example 2: Sales Tax
If you buy an item for $50 and the sales tax is 8%, how much will you pay in total?
- Sales tax amount = $50 * 0.08 = $4
- Total cost = $50 + $4 = $54
Thus, you will pay $54 in total.
Example 3: Exam Scores
If you scored 85 out of 100 on an exam, what is your percentage score?
- Percentage score = (85 / 100) * 100 = 85%
Hence, your score is 85%.
Advanced Applications in Data Analysis
Percentage calculations are fundamental in data analysis. Consider a dataset of customer demographics:
Scenario: Customer Demographics Analysis
Suppose you have data on 1000 customers, including their age groups:
- 18-25 years old: 200 customers
- 26-35 years old: 350 customers
- 36-45 years old: 250 customers
- 46-55 years old: 150 customers
- 56+ years old: 50 customers
To find the percentage of customers in each age group:
- 18-25 years old: (200 / 1000) * 100 = 20%
- 26-35 years old: (350 / 1000) * 100 = 35%
- 36-45 years old: (250 / 1000) * 100 = 25%
- 46-55 years old: (150 / 1000) * 100 = 15%
- 56+ years old: (50 / 1000) * 100 = 5%
This analysis helps understand the distribution of customers across different age groups.
Tips for Improving Accuracy
To ensure accuracy in percentage calculations:
- Double-Check Your Work: Always double-check your calculations to avoid errors.
- Use a Calculator: Use a calculator to perform calculations accurately.
- Keep Track of Decimal Places: Be mindful of decimal places and round appropriately.
- Understand the Context: Understand the context of the problem to avoid misinterpreting the question.
- Practice Regularly: Practice percentage calculations regularly to improve your skills.
Real-World Case Studies
Let's examine a couple of real-world case studies where percentage calculations are crucial:
Case Study 1: Retail Sales Analysis
A retail store wants to analyze its sales data to identify trends and improve its marketing strategies. By calculating the percentage of sales from different product categories, they can determine which products are most popular and which need more promotion. They can also calculate the percentage increase or decrease in sales over time to assess the effectiveness of their marketing campaigns.
Case Study 2: Financial Portfolio Management
An investor wants to manage their financial portfolio effectively. By calculating the percentage allocation of their assets across different investment types (e.g., stocks, bonds, real estate), they can ensure that their portfolio is diversified and aligned with their risk tolerance. They can also calculate the percentage return on their investments to assess their performance over time.
The Role of Percentages in Decision Making
Percentages play a vital role in decision-making across various domains. They provide a standardized way to compare different options and assess their relative merits. Whether you're evaluating investment opportunities, comparing prices, or analyzing data, understanding percentages is essential for making informed decisions.
By mastering the concepts and techniques discussed in this article, you can enhance your ability to interpret and utilize percentages effectively. Whether you're a student, a professional, or simply someone who wants to improve their financial literacy, a solid understanding of percentage calculations is a valuable asset.
Conclusion
Calculating what percent one number is of another is a fundamental skill with wide-ranging applications. By understanding the basic formula, avoiding common mistakes, and practicing regularly, you can master this skill and apply it to various real-world scenarios. Whether you're calculating discounts, analyzing data, or making financial decisions, percentages are a powerful tool for understanding and interpreting the world around you. In the case of 22 being a part of 126, we've determined that 22 is approximately 17.46% of 126, showcasing the practical application of these calculations.
Latest Posts
Latest Posts
-
6 A Forces In Simple Harmonic Motion
Nov 20, 2025
-
Unit 8 Homework 4 Answer Key
Nov 20, 2025
-
Unit 3 Worksheet Quantitative Energy Problems
Nov 20, 2025
-
Concept Map For Cirrhosis Of The Liver
Nov 20, 2025
-
The Confirmation Process For Federal Court Nominees Begins In The
Nov 20, 2025
Related Post
Thank you for visiting our website which covers about What Percent Of 126 Is 22 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.