What Is The Solution Of Log6x Log6 X 5 2
planetorganic
Nov 24, 2025 · 6 min read
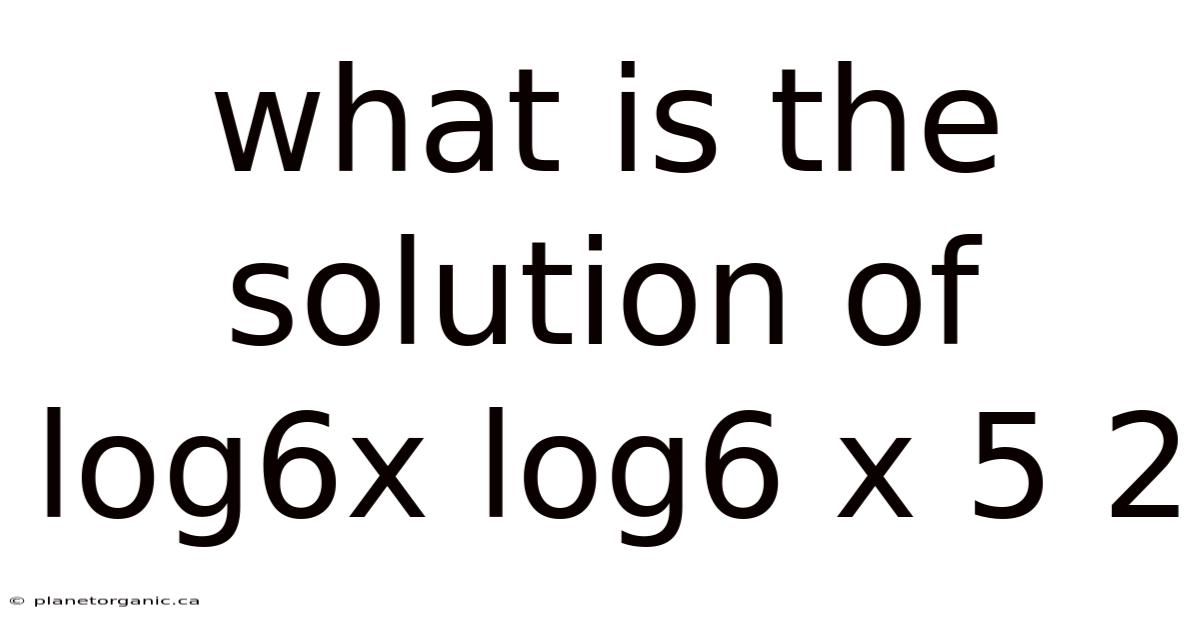
Table of Contents
Let's explore how to solve the equation log₆x * log₆x = 5 + 2. This equation involves logarithms, and finding its solution requires a clear understanding of logarithmic properties and algebraic manipulation. We will break down the steps, explain the underlying principles, and provide a comprehensive guide to finding the solution.
Understanding Logarithms
Before diving into the solution, let's revisit some fundamental concepts about logarithms. A logarithm is the inverse operation to exponentiation. Specifically, if b<sup>y</sup> = x, then log<sub>b</sub>(x) = y. In simpler terms, the logarithm of a number x with base b is the exponent to which b must be raised to produce x.
Key properties of logarithms include:
- Product Rule: log<sub>b</sub>(mn) = log<sub>b</sub>(m) + log<sub>b</sub>(n)
- Quotient Rule: log<sub>b</sub>(m/ n) = log<sub>b</sub>(m) - log<sub>b</sub>(n)
- Power Rule: log<sub>b</sub>(m<sup>p</sup>) = p log<sub>b</sub>(m)
- Change of Base Formula: log<sub>b</sub>(x) = log<sub>a</sub>(x) / log<sub>a</sub>(b)
In our case, we're dealing with log base 6, denoted as log₆.
Problem Statement
We are tasked with solving the equation:
log₆x * log₆x = 5 + 2
Which simplifies to:
(log₆x)² = 7
Step-by-Step Solution
Here's how we can solve this equation step-by-step:
Step 1: Take the Square Root of Both Sides
To isolate the logarithmic term, we take the square root of both sides of the equation:
√((log₆x)²) = ±√7
This gives us:
log₆x = ±√7
Step 2: Convert the Logarithmic Equation to Exponential Form
Now, we convert the logarithmic equation into its equivalent exponential form. Recall that log<sub>b</sub>(x) = y is equivalent to b<sup>y</sup> = x. Therefore:
For log₆x = √7, we have x = 6<sup>√7</sup>
For log₆x = -√7, we have x = 6<sup>-√7</sup>
Step 3: Simplify the Solutions
We now have two potential solutions for x:
x = 6<sup>√7</sup> and x = 6<sup>-√7</sup>
We can rewrite 6<sup>-√7</sup> as 1 / 6<sup>√7</sup>.
Step 4: Verify the Solutions
It's crucial to verify whether these solutions are valid by plugging them back into the original equation.
For x = 6<sup>√7</sup>:
(log₆(6<sup>√7</sup>))² = (√7)² = 7, which matches the right side of the original equation.
For x = 6<sup>-√7</sup>:
(log₆(6<sup>-√7</sup>))² = (-√7)² = 7, which also matches the right side of the original equation.
Both solutions are valid.
Step 5: State the Final Solutions
The solutions to the equation (log₆x)² = 7 are:
x = 6<sup>√7</sup> and x = 6<sup>-√7</sup>
Practical Implications and Applications
Understanding logarithmic equations is vital in many fields, including:
- Finance: Calculating compound interest and loan payments.
- Physics: Analyzing radioactive decay and sound intensity.
- Chemistry: Determining pH levels and reaction rates.
- Computer Science: Analyzing algorithm complexity (e.g., binary search).
- Engineering: Solving problems related to signal processing and control systems.
Logarithms help compress large ranges of values into manageable scales, making them essential tools for data analysis and modeling.
Advanced Concepts and Extensions
Change of Base
In some cases, you might encounter logarithms with different bases. To solve such equations, it's often necessary to use the change of base formula:
log<sub>b</sub>(x) = log<sub>a</sub>(x) / log<sub>a</sub>(b)
This formula allows you to convert logarithms from one base to another, making it easier to combine and simplify equations.
Logarithmic Identities
Mastering logarithmic identities is crucial for simplifying complex expressions. Some useful identities include:
- log<sub>b</sub>(1) = 0
- log<sub>b</sub>(b) = 1
- log<sub>b</sub>(b<sup>x</sup>) = x
- b<sup>log<sub>b</sub>(x)</sup> = x
These identities can significantly simplify logarithmic equations and make them easier to solve.
Graphical Interpretation
Logarithmic equations can also be analyzed graphically. The graph of a logarithmic function y = log<sub>b</sub>(x) has a vertical asymptote at x = 0 and passes through the point (1, 0). The shape of the graph depends on the base b. By graphing the logarithmic function and analyzing its intersections with other curves, you can gain insights into the solutions of logarithmic equations.
Common Mistakes to Avoid
When solving logarithmic equations, be aware of common pitfalls:
- Forgetting to Check for Extraneous Solutions: Always verify your solutions by plugging them back into the original equation. Logarithmic functions are only defined for positive arguments, so any solution that results in a negative or zero argument is extraneous.
- Incorrectly Applying Logarithmic Properties: Make sure you understand and apply the logarithmic properties correctly. A common mistake is to assume that log<sub>b</sub>(m + n) = log<sub>b</sub>(m) + log<sub>b</sub>(n), which is incorrect.
- Ignoring the Domain of Logarithmic Functions: Remember that the argument of a logarithmic function must be positive. Always consider the domain when solving logarithmic equations.
FAQs About Solving Logarithmic Equations
Q1: What is a logarithm?
A1: A logarithm is the inverse operation to exponentiation. If b<sup>y</sup> = x, then log<sub>b</sub>(x) = y.
Q2: How do you solve a logarithmic equation?
A2: To solve a logarithmic equation, first isolate the logarithmic term, then convert the equation to exponential form, and finally solve for the variable. Always check your solutions to ensure they are valid.
Q3: What is the change of base formula, and when should I use it?
A3: The change of base formula is log<sub>b</sub>(x) = log<sub>a</sub>(x) / log<sub>a</sub>(b). Use it when you need to convert logarithms from one base to another, especially when dealing with different bases in the same equation.
Q4: Why is it important to check for extraneous solutions?
A4: It is important to check for extraneous solutions because logarithmic functions are only defined for positive arguments. Solutions that result in negative or zero arguments are not valid.
Q5: Can a logarithmic equation have more than one solution?
A5: Yes, a logarithmic equation can have more than one solution, as demonstrated in our example where we found two solutions: x = 6<sup>√7</sup> and x = 6<sup>-√7</sup>.
Q6: What are some real-world applications of logarithmic equations?
A6: Logarithmic equations have numerous real-world applications in fields such as finance, physics, chemistry, computer science, and engineering. They are used to model and analyze phenomena involving exponential growth or decay.
Conclusion
Solving the equation (log₆x)² = 7 involves understanding the fundamental properties of logarithms, algebraic manipulation, and careful verification of solutions. By converting the logarithmic equation to exponential form and considering both positive and negative roots, we found two valid solutions: x = 6<sup>√7</sup> and x = 6<sup>-√7</sup>. Mastering these techniques enables you to tackle a wide range of logarithmic equations and apply them in various practical contexts. Logarithmic equations are not just abstract mathematical concepts; they are powerful tools for understanding and modeling the world around us. Embrace the challenge, practice regularly, and unlock the full potential of logarithms in your problem-solving toolkit.
Latest Posts
Latest Posts
-
Cannot Use Import Statement Outside A Module
Nov 24, 2025
-
Which Sentences Contain A Relative Clause Choose Three Answers
Nov 24, 2025
-
Investigating The Ph Scale Answer Key
Nov 24, 2025
-
Mark Klimek Lecture 12 Prioritization And Delegation
Nov 24, 2025
-
What Is An Example Of A Non Deposit Institution
Nov 24, 2025
Related Post
Thank you for visiting our website which covers about What Is The Solution Of Log6x Log6 X 5 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.