What Is 80 Percent Of 36
planetorganic
Nov 22, 2025 · 8 min read
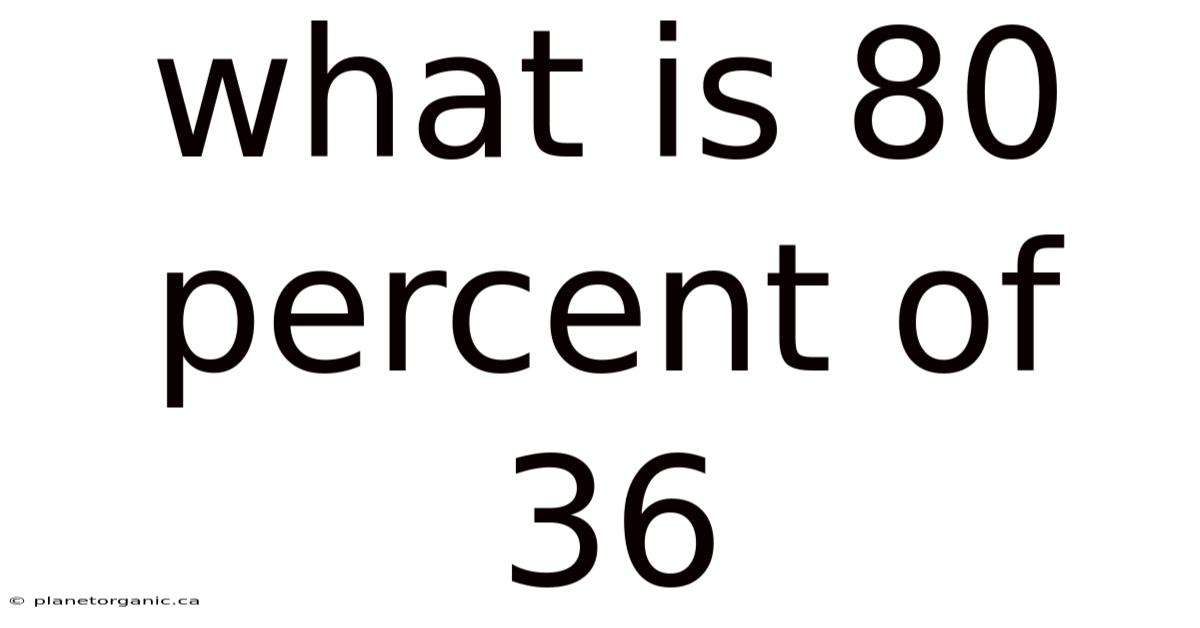
Table of Contents
Calculating percentages is a fundamental skill with applications in everyday life, from figuring out discounts at the store to calculating tips at a restaurant. When we want to find what 80 percent of 36 is, we are essentially determining a portion of a whole. This seemingly simple calculation is a gateway to understanding more complex mathematical concepts and practical problem-solving.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The term "percent" comes from the Latin per centum, meaning "per hundred." Thus, 80 percent means 80 out of every 100. Percentages are used to describe proportions, ratios, or fractions in a standardized way, making it easy to compare different quantities.
Converting Percentage to Decimal
To calculate 80 percent of 36, the first step is to convert the percentage into a decimal. This conversion is necessary because we cannot directly multiply a percentage with a number. To convert a percentage to a decimal, we divide the percentage by 100.
In this case, we convert 80 percent to a decimal:
80 ÷ 100 = 0.8
The Calculation
Now that we have converted 80 percent into its decimal form (0.8), we can proceed with the calculation. To find 80 percent of 36, we multiply 36 by 0.8:
36 × 0.8 = 28.8
Therefore, 80 percent of 36 is 28.8.
Alternative Methods
There are several alternative methods to calculate 80 percent of 36. Understanding these methods can provide a deeper understanding of percentages and improve your problem-solving skills.
Method 1: Using Fractions
Another way to find 80 percent of 36 is by converting the percentage to a fraction. 80 percent can be expressed as the fraction 80/100. This fraction can be simplified by dividing both the numerator and the denominator by their greatest common divisor, which is 20.
80/100 = (80 ÷ 20) / (100 ÷ 20) = 4/5
Now, to find 80 percent of 36, we multiply 36 by the fraction 4/5:
36 × (4/5) = (36 × 4) / 5 = 144 / 5 = 28.8
Method 2: Breaking Down the Percentage
Another approach is to break down 80 percent into smaller, more manageable parts. For example, we can express 80 percent as the sum of 50 percent and 30 percent. Finding 50 percent of 36 is straightforward:
50 percent of 36 = 36 ÷ 2 = 18
Next, we find 30 percent of 36. To do this, we can first find 10 percent of 36 and then multiply the result by 3:
10 percent of 36 = 36 ÷ 10 = 3.6 30 percent of 36 = 3.6 × 3 = 10.8
Finally, we add the two results together:
50 percent of 36 + 30 percent of 36 = 18 + 10.8 = 28.8
Method 3: Using Proportions
We can also use proportions to solve this problem. A proportion is an equation that states that two ratios are equal. In this case, we can set up the following proportion:
80/100 = x/36
Here, x represents 80 percent of 36. To solve for x, we can cross-multiply:
80 × 36 = 100 × x 2880 = 100x
Now, we divide both sides by 100 to isolate x:
x = 2880 ÷ 100 = 28.8
Real-World Applications
Understanding how to calculate percentages is essential in many real-world scenarios. Here are some common applications:
Discounts and Sales
When shopping, percentages are often used to express discounts. For example, if an item is marked as 20 percent off, calculating the discount amount helps determine the final price. If an item costs $36 and there is a 20 percent discount, the discount amount is:
20 percent of $36 = 0.20 × $36 = $7.20
The final price of the item would then be:
$36 - $7.20 = $28.80
Calculating Tips
In restaurants and other service industries, tipping is a common practice. Tips are usually calculated as a percentage of the total bill. For instance, if the bill is $36 and you want to leave a 20 percent tip:
20 percent of $36 = 0.20 × $36 = $7.20
Interest Rates
Percentages are fundamental in finance, especially when dealing with interest rates. Whether it's the interest earned on a savings account or the interest charged on a loan, understanding percentages is crucial. For example, if you have $36 in a savings account with an annual interest rate of 5 percent:
Annual interest earned = 5 percent of $36 = 0.05 × $36 = $1.80
Taxes
Taxes are often calculated as a percentage of income or sales. For instance, if a sales tax is 8 percent and you purchase an item for $36:
Sales tax amount = 8 percent of $36 = 0.08 × $36 = $2.88
The total cost of the item would then be:
$36 + $2.88 = $38.88
Statistics
Percentages are widely used in statistics to express proportions and rates. For example, if a survey finds that 80 percent of 36 people prefer a certain product:
Number of people who prefer the product = 80 percent of 36 = 0.80 × 36 = 28.8
Since we can't have a fraction of a person, we would round this to the nearest whole number, which is approximately 29 people.
Common Mistakes to Avoid
When calculating percentages, it's important to avoid common mistakes that can lead to incorrect answers. Here are some pitfalls to watch out for:
Forgetting to Convert Percentage to Decimal or Fraction
One of the most common mistakes is forgetting to convert the percentage to a decimal or fraction before performing the calculation. Multiplying a number directly by the percentage value without converting it will result in a wrong answer.
Misunderstanding the Base Number
Ensure you are clear about what number you are taking the percentage of. For example, if a store offers a 30 percent discount on an item and then an additional 10 percent off the discounted price, you can't simply add the percentages together. The 10 percent is calculated on the new, lower price, not the original price.
Rounding Errors
When dealing with decimals, rounding too early in the calculation can lead to inaccuracies. It is best to keep as many decimal places as possible until the final answer and then round appropriately.
Confusing Increase and Decrease
When calculating percentage increases or decreases, be careful to apply the percentage to the correct base number. For instance, if a price increases by 20 percent and then decreases by 20 percent, the final price will not be the same as the original price.
Complex Percentage Problems
While finding 80 percent of 36 is a relatively simple calculation, percentages can also be used in more complex problems. Here are a few examples:
Calculating Percentage Change
To calculate the percentage change between two values, you use the formula:
Percentage Change = [(New Value - Old Value) / Old Value] × 100
For example, if a price increases from $36 to $45:
Percentage Change = [($45 - $36) / $36] × 100 = (9 / 36) × 100 = 0.25 × 100 = 25%
Finding the Original Value
Sometimes, you might need to find the original value when you know the percentage and the result. For example, if 20 percent of a number is 36, you can find the original number by setting up the equation:
- 20 × Original Number = 36 Original Number = 36 / 0.20 = 180
Compound Interest
Compound interest involves earning interest on the principal amount as well as on the accumulated interest. The formula for compound interest is:
A = P (1 + r/n)^(nt)
Where:
- A = the future value of the investment/loan, including interest
- P = the principal investment amount (the initial deposit or loan amount)
- r = the annual interest rate (as a decimal)
- n = the number of times that interest is compounded per year
- t = the number of years the money is invested or borrowed for
For example, if you invest $36 at an annual interest rate of 5 percent compounded annually for 10 years:
A = $36 (1 + 0.05/1)^(1*10) = $36 (1.05)^10 ≈ $58.63
Tips and Tricks
Here are some useful tips and tricks to make percentage calculations easier:
Use Benchmarks
Memorizing common percentage benchmarks can speed up calculations. For example:
- 10% of a number is the number divided by 10.
- 25% of a number is the number divided by 4.
- 50% of a number is the number divided by 2.
- 75% of a number is 3/4 of the number.
Estimate
Before calculating, estimate the answer to check if your final result is reasonable. For example, if you are finding 80 percent of 36, you know the answer should be less than 36 but more than half of 36.
Use a Calculator
For complex calculations or when accuracy is critical, use a calculator. Most calculators have a percentage function that simplifies the process.
Practice Regularly
The best way to improve your percentage calculation skills is to practice regularly. Try solving various percentage problems and applying them in real-life situations.
Conclusion
Calculating percentages is a fundamental skill with wide-ranging applications in everyday life. Whether you are figuring out discounts, calculating tips, understanding interest rates, or interpreting statistics, a solid understanding of percentages is essential. By converting percentages to decimals or fractions, breaking down percentages into smaller parts, using proportions, and avoiding common mistakes, you can master percentage calculations and apply them confidently in various contexts. Remembering that 80 percent of 36 is 28.8 is just the beginning; the key is to understand how you arrive at that answer and to be able to apply that understanding to other problems. Regular practice and a clear grasp of the underlying concepts will ensure that you are well-equipped to handle any percentage-related challenge that comes your way.
Latest Posts
Latest Posts
-
What Was True Of The Government Under The Roman Empire
Nov 22, 2025
-
Evidence Of Evolution Homologous Structures Worksheet Answers
Nov 22, 2025
-
Which Term Is Paired Correctly With Its Definition
Nov 22, 2025
-
Amoeba Sisters Video Recap Prokaryotic Vs Eukaryotic Cells Answer Sheet
Nov 22, 2025
-
Which Of The Following Statements Displays The Speakers Unfair Bias
Nov 22, 2025
Related Post
Thank you for visiting our website which covers about What Is 80 Percent Of 36 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.