What Is 8 To The Power Of 2
planetorganic
Nov 16, 2025 · 8 min read
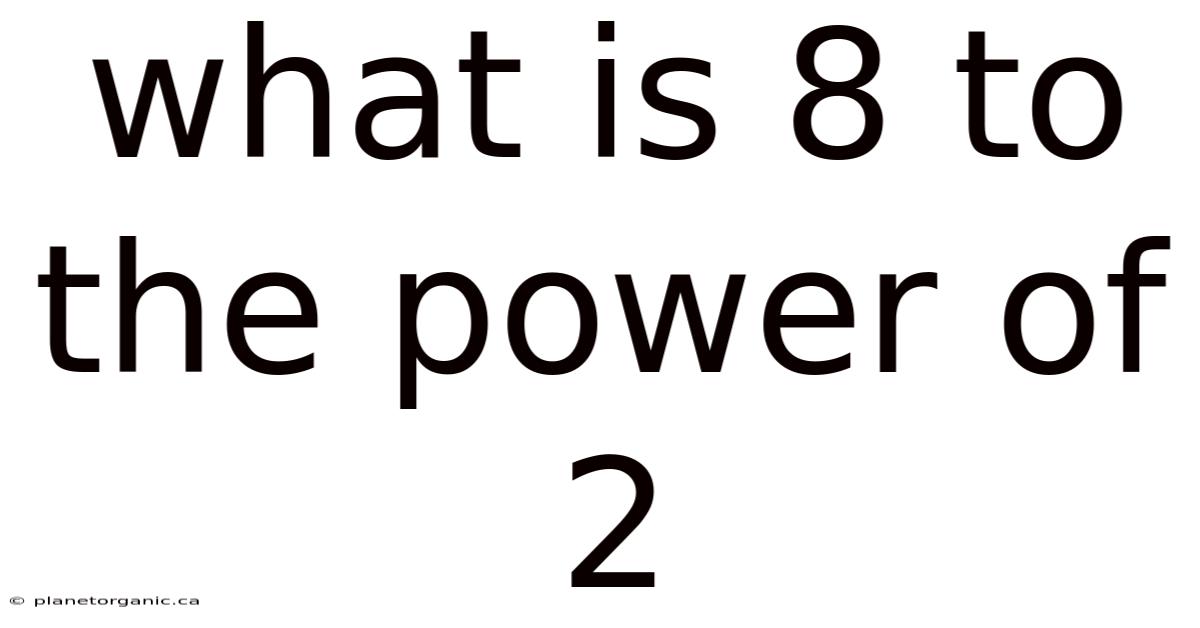
Table of Contents
The power of exponents unveils fascinating patterns in mathematics, allowing us to express repeated multiplication concisely. When we delve into "8 to the power of 2," we're exploring a fundamental concept with broad applications.
Unveiling 8 to the Power of 2
"8 to the power of 2," often written as 8², signifies multiplying 8 by itself. In essence, it means 8 * 8. This operation yields a result that's both straightforward and significant in various mathematical contexts.
The Calculation: A Simple Multiplication
To calculate 8², we simply multiply 8 by itself:
8 * 8 = 64
Therefore, 8 to the power of 2 equals 64.
Understanding Exponents: A Broader Perspective
Before we dive deeper, let's understand the fundamental concept of exponents. An exponent indicates how many times a number (the base) is multiplied by itself. In the expression aⁿ, 'a' is the base, and 'n' is the exponent.
- Base: The number being multiplied.
- Exponent: The number indicating how many times the base is multiplied by itself.
In the case of 8², 8 is the base, and 2 is the exponent. This signifies that 8 is multiplied by itself twice.
The Significance of Squaring
Raising a number to the power of 2 is commonly referred to as "squaring" the number. The term originates from geometry, where the area of a square is calculated by squaring the length of one of its sides. For example, a square with sides of length 8 has an area of 64 (8 * 8).
The Mathematical Properties of Exponents
Exponents possess several key properties that simplify complex calculations and provide valuable insights into mathematical relationships.
Product of Powers
When multiplying powers with the same base, you add the exponents:
aⁿ * aᵐ = aⁿ⁺ᵐ
For example:
2² * 2³ = 2^(2+3) = 2⁵ = 32
Quotient of Powers
When dividing powers with the same base, you subtract the exponents:
aⁿ / aᵐ = aⁿ⁻ᵐ
For example:
3⁵ / 3² = 3^(5-2) = 3³ = 27
Power of a Power
When raising a power to another power, you multiply the exponents:
(aⁿ)ᵐ = aⁿ*ᵐ
For example:
(4²)³ = 4^(2*3) = 4⁶ = 4096
Power of a Product
The power of a product is the product of the powers:
(ab)ⁿ = aⁿbⁿ
For example:
(2 * 3)² = 2² * 3² = 4 * 9 = 36
Power of a Quotient
The power of a quotient is the quotient of the powers:
(a/b)ⁿ = aⁿ / bⁿ
For example:
(6/2)² = 6² / 2² = 36 / 4 = 9
Zero Exponent
Any non-zero number raised to the power of 0 is 1:
a⁰ = 1 (where a ≠ 0)
For example:
5⁰ = 1
Negative Exponent
A number raised to a negative exponent is the reciprocal of the number raised to the positive exponent:
a⁻ⁿ = 1 / aⁿ
For example:
2⁻² = 1 / 2² = 1 / 4 = 0.25
Fractional Exponents
Fractional exponents represent roots. For example, a^(1/n) is the nth root of a:
a^(1/n) = ⁿ√a
For example:
9^(1/2) = √9 = 3
The Applications of 8 to the Power of 2
The concept of "8 to the power of 2," or 8 squared, finds its applications in various domains, ranging from basic geometry to more advanced fields of study.
Geometry
As previously mentioned, squaring a number is directly related to finding the area of a square. If you have a square with each side measuring 8 units, the area is 8² = 64 square units. This is a fundamental concept in calculating areas and volumes.
Algebra
In algebra, understanding squares is essential for solving quadratic equations, simplifying expressions, and working with polynomials. For example, when dealing with quadratic expressions such as x² + 4x + 4, recognizing perfect squares (like (x+2)²) is crucial for factoring and simplifying.
Computer Science
In computer science, the concept of powers of 2 is particularly important due to the binary nature of digital systems. Memory sizes, data storage capacities, and processing speeds are often based on powers of 2. While 8 itself isn't a power of 2, understanding how squaring works is essential when dealing with memory allocation, image processing, and more.
For instance, if you are working with pixel data, each color channel (red, green, blue) often has 8 bits of information, which means each channel can represent 2^8 = 256 different levels of intensity. Squaring operations are fundamental in image processing and data manipulation.
Physics
In physics, squares appear in various formulas, such as in kinetic energy (KE = 1/2 mv²) and the inverse square law (e.g., gravitational force and electromagnetic radiation). The presence of a squared term in a formula indicates that the quantity it's describing changes proportionally to the square of another quantity. Understanding such relationships is vital in fields like mechanics and electromagnetism.
Finance
In finance, concepts like compound interest involve powers and exponents. While 8 to the power of 2 may not be directly used in a specific formula, understanding how values increase exponentially is essential when calculating returns on investments or analyzing financial growth.
Real-World Examples
Let's look at some practical examples where understanding "8 to the power of 2" is useful:
- Area Calculation: If you're designing a square garden plot and each side is 8 meters long, you would calculate the area as 8² = 64 square meters to determine how much soil you need.
- Pixel Count: If you're working with a small display that has a resolution of 8x8 pixels, the total number of pixels is 8² = 64 pixels.
- Engineering Design: Engineers use squares in various calculations, such as determining the stress on a material or the flow rate in a pipe. For example, the area of a square duct with sides of 8 inches would be 64 square inches.
How to Calculate Higher Powers
While 8² is straightforward, let's explore how to calculate higher powers of 8:
- 8³ (8 to the power of 3): 8 * 8 * 8 = 512
- 8⁴ (8 to the power of 4): 8 * 8 * 8 * 8 = 4096
- 8⁵ (8 to the power of 5): 8 * 8 * 8 * 8 * 8 = 32768
As you can see, the numbers grow rapidly as the exponent increases.
Practical Tips for Working with Exponents
Here are some practical tips to make working with exponents easier:
- Memorize Common Squares: Knowing squares of numbers up to 20 (e.g., 1² = 1, 2² = 4, 3² = 9, ..., 20² = 400) can significantly speed up calculations.
- Use a Calculator: For larger exponents or complex calculations, a calculator is your best friend. Most calculators have a dedicated exponentiation function (usually denoted as x^y or a similar symbol).
- Break Down Complex Calculations: If you're faced with a complex expression involving exponents, break it down into smaller, more manageable parts. Apply the properties of exponents to simplify the expression.
- Practice Regularly: Practice makes perfect. The more you work with exponents, the more comfortable and confident you'll become.
Common Mistakes to Avoid
When working with exponents, it's easy to make mistakes. Here are some common pitfalls to avoid:
- Misunderstanding the Order of Operations: Remember PEMDAS/BODMAS (Parentheses/Brackets, Exponents/Orders, Multiplication and Division, Addition and Subtraction). Exponents come before multiplication, division, addition, and subtraction.
- Confusing a Negative Base with a Negative Exponent: For example, (-2)² = 4, but 2⁻² = 1/4. The parentheses are crucial when dealing with negative bases.
- Incorrectly Applying the Properties of Exponents: Double-check that you are applying the correct properties when simplifying expressions. For instance, a common mistake is to assume that (a + b)² = a² + b², which is incorrect. The correct expansion is (a + b)² = a² + 2ab + b².
- Forgetting to Distribute the Exponent: When raising a product or quotient to a power, remember to apply the exponent to each factor or term. For example, (2x)² = 4x², not 2x².
Advanced Concepts Related to Exponents
Understanding exponents opens the door to more advanced mathematical concepts.
Exponential Functions
An exponential function is a function in which the independent variable (x) appears in the exponent. The general form is:
f(x) = aˣ
where a is a constant (the base) and x is the exponent. Exponential functions are used to model phenomena that grow or decay at a rate proportional to their current value, such as population growth, radioactive decay, and compound interest.
Logarithms
Logarithms are the inverse of exponential functions. If aˣ = y, then the logarithm base a of y is x, written as:
logₐ(y) = x
Logarithms are used to solve equations in which the unknown variable is in the exponent, and they are also used in various fields such as physics, engineering, and computer science.
Complex Exponents
Exponents can also be complex numbers. The most famous example is Euler's formula:
e^(ix) = cos(x) + i sin(x)
where e is the base of the natural logarithm, i is the imaginary unit (√-1), and x is a real number. This formula connects exponential functions with trigonometric functions and is fundamental in complex analysis.
Exponentiation in Abstract Algebra
In abstract algebra, exponentiation is generalized to apply to elements of various algebraic structures, such as groups and rings. The exponent represents repeated application of an operation defined on the structure.
Conclusion
"8 to the power of 2," or 8 squared, is a fundamental mathematical operation that serves as a building block for more complex concepts. It's not just about multiplying 8 by itself to get 64; it's about understanding the broader implications of exponents in mathematics, science, and technology. Whether you're calculating the area of a square, simplifying algebraic expressions, or working with data in computer science, a solid grasp of exponents is essential. By understanding the properties of exponents and practicing regularly, you can unlock a deeper understanding of the mathematical world.
Latest Posts
Latest Posts
-
2 5 3 Practice Modeling Wildlife Sanctuary Answers
Nov 16, 2025
-
Stimulus Diffusion Ap Human Geography Definition
Nov 16, 2025
-
Anatomy And Physiology Coloring Workbook Body Tissues
Nov 16, 2025
-
The Alpha Prince And His Bride Full Story Free Download
Nov 16, 2025
-
Insurance Companies Practice To Distribute Risk Among Many Policyholders
Nov 16, 2025
Related Post
Thank you for visiting our website which covers about What Is 8 To The Power Of 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.