Six More Than Three Times A Number W
planetorganic
Nov 11, 2025 · 10 min read
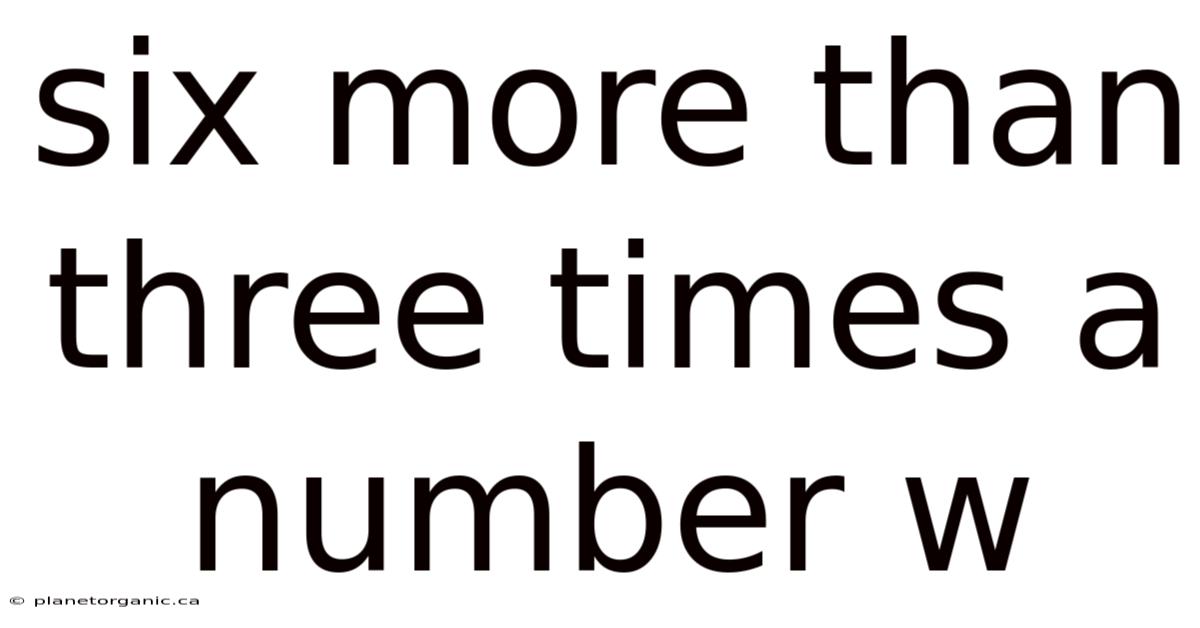
Table of Contents
Six more than three times a number: This simple phrase encapsulates a world of algebraic expressions, ready to be explored and understood. Whether you're a student just starting your algebra journey or someone looking to refresh your skills, understanding how to translate this kind of phrase into a mathematical equation is fundamental. This article provides a comprehensive breakdown of how to interpret and solve equations involving phrases like "six more than three times a number," ensuring clarity and confidence in your algebraic abilities.
Understanding the Basics
Before we dive into complex problems, it's important to understand the basic concepts involved. Algebraic expressions are combinations of numbers, variables, and mathematical operations. They are used to represent relationships and quantities in a concise and general way. Let's break down the key components:
- Variable: A variable is a symbol (usually a letter) that represents an unknown number. Commonly used variables include x, y, and z.
- Constant: A constant is a fixed number that does not change its value. For example, 6, 3, and -5 are all constants.
- Coefficient: A coefficient is a number that multiplies a variable. For instance, in the term 3x, 3 is the coefficient.
- Operation: Operations are mathematical processes like addition (+), subtraction (-), multiplication (*), and division (/).
Translating verbal phrases into algebraic expressions involves recognizing the mathematical operations implied by the words. Here are some common phrases and their algebraic equivalents:
- "A number increased by 5" translates to x + 5.
- "Twice a number" translates to 2x.
- "A number decreased by 3" translates to x - 3.
- "Half of a number" translates to x/2 or (1/2)x.
Translating "Six More Than Three Times a Number"
Now, let's focus on the specific phrase "six more than three times a number." This phrase can be broken down into smaller parts:
- "A number": This indicates the unknown, which we can represent with the variable x.
- "Three times a number": This means we multiply the variable x by 3, resulting in 3x.
- "Six more than": This means we add 6 to the previous result.
Putting it all together, the algebraic expression for "six more than three times a number" is:
3x + 6
This expression tells us that whatever the value of x is, we first multiply it by 3 and then add 6 to get the final result.
Constructing Equations
An equation is a statement that two expressions are equal. It includes an equals sign (=) between the two expressions. To form an equation, we need to equate our algebraic expression to a specific value or another expression.
For example, if we are told that "six more than three times a number is equal to 21," we can write the equation as:
3x + 6 = 21
This equation states that the expression 3x + 6 has the same value as 21.
Solving Linear Equations
Solving an equation means finding the value of the variable that makes the equation true. To solve the equation 3x + 6 = 21, we need to isolate x on one side of the equation. This involves using inverse operations to undo the operations performed on x.
Here are the steps to solve the equation 3x + 6 = 21:
-
Subtract 6 from both sides:
3x + 6 - 6 = 21 - 6
3x = 15
-
Divide both sides by 3:
(3x)/3 = 15/3
x = 5
Therefore, the solution to the equation 3x + 6 = 21 is x = 5. This means that if we substitute 5 for x in the original equation, the equation holds true:
3(5) + 6 = 15 + 6 = 21
More Examples and Practice Problems
To solidify your understanding, let's work through some additional examples and practice problems:
Example 1:
Problem: "Six more than three times a number is equal to 30. Find the number."
Solution:
- Write the equation: 3x + 6 = 30
- Subtract 6 from both sides: 3x = 24
- Divide both sides by 3: x = 8
Thus, the number is 8.
Example 2:
Problem: "If six more than three times a number is the same as fifteen less than six times the number, what is the number?"
Solution:
- Write the expressions:
- "Six more than three times a number": 3x + 6
- "Fifteen less than six times the number": 6x - 15
- Write the equation: 3x + 6 = 6x - 15
- Subtract 3x from both sides: 6 = 3x - 15
- Add 15 to both sides: 21 = 3x
- Divide both sides by 3: x = 7
Thus, the number is 7.
Example 3:
Problem: "The result of adding six to three times a certain number is the same as multiplying the sum of the number and two by five. Find the number."
Solution:
- Write the expressions:
- "Adding six to three times a certain number": 3x + 6
- "Multiplying the sum of the number and two by five": 5(x + 2)
- Write the equation: 3x + 6 = 5(x + 2)
- Distribute the 5 on the right side: 3x + 6 = 5x + 10
- Subtract 3x from both sides: 6 = 2x + 10
- Subtract 10 from both sides: -4 = 2x
- Divide both sides by 2: x = -2
Thus, the number is -2.
Practice Problems:
- Six more than three times a number is 42. Find the number.
- If six more than three times a number is equal to two times the number plus eleven, what is the number?
- The result of adding six to three times a number is equal to the number increased by ten. Find the number.
Advanced Concepts: Inequalities
Inequalities are similar to equations but use inequality symbols to compare expressions. The most common inequality symbols are:
- > (greater than)
- < (less than)
- ≥ (greater than or equal to)
- ≤ (less than or equal to)
For example, the inequality "six more than three times a number is greater than 18" can be written as:
3x + 6 > 18
To solve inequalities, we follow similar steps as solving equations, but with one key difference: if we multiply or divide both sides of an inequality by a negative number, we must reverse the direction of the inequality symbol.
Here's how to solve the inequality 3x + 6 > 18:
-
Subtract 6 from both sides:
3x > 12
-
Divide both sides by 3:
x > 4
This means that any value of x greater than 4 will satisfy the inequality.
Real-World Applications
Understanding how to translate phrases into algebraic expressions and solve equations is not just a theoretical exercise. It has practical applications in various real-world scenarios.
Example 1:
Problem: A phone company charges a monthly fee of $6 plus $3 for each gigabyte of data used. If your total bill is $27, how many gigabytes of data did you use?
Solution:
- Let x be the number of gigabytes used.
- Write the equation: 3x + 6 = 27
- Subtract 6 from both sides: 3x = 21
- Divide both sides by 3: x = 7
You used 7 gigabytes of data.
Example 2:
Problem: You have $6 and you want to buy movie tickets that cost $3 each. How many tickets can you buy?
Solution:
This is a bit of a trick question designed to highlight the context of the problem. While we could set up an inequality, the practical answer is limited by the fact that you can't buy a fraction of a ticket. Since you already have $6, let's say you want to know how many more dollars you need to buy a certain number of tickets.
Let x be the number of additional dollars you need. Let's say t is the number of tickets you want to buy. The total cost of the tickets would be 3t. Your current financial situation means:
3t = 6 + x
If x = 0, you want to know how many tickets you can buy exactly. 3t = 6 t = 2
You can buy 2 tickets. If you wanted to buy 3 tickets, then x would be 3: 33 = 6 + x 9 = 6 + x x = 3
You would need an additional $3.
Example 3:
Problem: A rectangular garden has a width of x meters. The length is six meters more than three times the width. If the perimeter of the garden is 52 meters, find the width and length.
Solution:
- Write the expressions:
- Width: x
- Length: 3x + 6
- The perimeter of a rectangle is given by the formula: P = 2(length + width)
- Write the equation: 2(x + 3x + 6) = 52
- Simplify: 2(4x + 6) = 52
- Distribute the 2: 8x + 12 = 52
- Subtract 12 from both sides: 8x = 40
- Divide both sides by 8: x = 5
Thus, the width is 5 meters.
Now, find the length:
Length = 3x + 6 = 3(5) + 6 = 15 + 6 = 21
Thus, the length is 21 meters.
Common Mistakes to Avoid
When translating and solving algebraic equations, there are several common mistakes that students often make. Here are some tips to avoid them:
- Misinterpreting the order of operations: Always follow the correct order of operations (PEMDAS/BODMAS): Parentheses/Brackets, Exponents/Orders, Multiplication and Division (from left to right), and Addition and Subtraction (from left to right).
- Incorrectly distributing: When distributing a number across parentheses, make sure to multiply it by every term inside the parentheses. For example, 5(x + 2) = 5x + 10, not 5x + 2.
- Forgetting to perform the same operation on both sides: To maintain the equality of an equation, always perform the same operation on both sides. If you add 5 to one side, you must add 5 to the other side as well.
- Incorrectly combining like terms: Only combine terms that have the same variable and exponent. For example, 3x + 2x = 5x, but 3x + 2x^2 cannot be combined.
- Reversing the inequality symbol incorrectly: Remember to reverse the inequality symbol only when multiplying or dividing both sides by a negative number.
Tips for Success
To excel in algebra and effectively solve problems involving phrases like "six more than three times a number," consider the following tips:
- Practice regularly: The more you practice, the more comfortable and confident you will become with translating phrases and solving equations.
- Break down complex problems: Divide complex problems into smaller, more manageable steps.
- Check your work: After solving an equation, substitute your solution back into the original equation to verify that it is correct.
- Seek help when needed: Don't hesitate to ask for help from teachers, tutors, or classmates if you are struggling with a particular concept or problem.
- Use visual aids: Diagrams, charts, and other visual aids can help you better understand and visualize algebraic concepts.
Conclusion
Understanding how to translate phrases like "six more than three times a number" into algebraic expressions and solve equations is a fundamental skill in algebra. By mastering the basic concepts, practicing regularly, and avoiding common mistakes, you can build a strong foundation in algebra and confidently tackle more complex problems. Remember to break down problems into smaller steps, check your work, and seek help when needed. With consistent effort and the right approach, you can achieve success in algebra and apply your skills to real-world scenarios.
Latest Posts
Latest Posts
-
Formula To Reference Cell A1 From The Alpha Worksheet
Nov 11, 2025
-
200 Question Sample Physical Therapy Exam Pdf
Nov 11, 2025
-
Which Of The Following Undergoes Solvolysis In Methanol Most Rapidly
Nov 11, 2025
-
Determine The Maturity Date And Compute Interest For Each Note
Nov 11, 2025
-
In 1992 The European Union Mandated A
Nov 11, 2025
Related Post
Thank you for visiting our website which covers about Six More Than Three Times A Number W . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.