7 Is Ten Times The Value Of What Number
planetorganic
Nov 14, 2025 · 9 min read
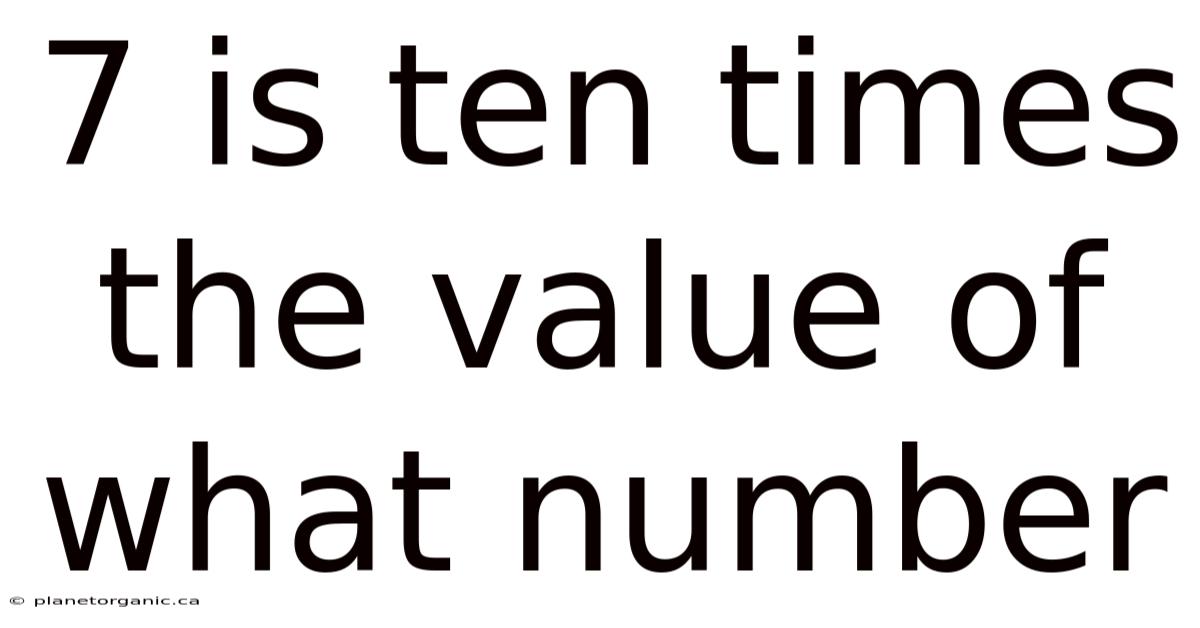
Table of Contents
Understanding place value is fundamental to grasping mathematical concepts, and the question "7 is ten times the value of what number?" serves as a valuable exercise in reinforcing this understanding. This article will delve into the intricacies of place value, explore different methods to solve this problem, provide real-world applications, and address common misconceptions. Whether you're a student seeking clarification, a teacher looking for resources, or simply curious about the topic, this comprehensive guide will offer a clear and insightful explanation.
Decoding Place Value: The Foundation
At its core, the question hinges on the concept of place value. Place value is the numerical value that a digit has by virtue of its position in a number. In our base-ten (decimal) system, each place represents a power of ten.
Here’s a breakdown:
- Ones place: The rightmost digit represents the number of ones (10⁰).
- Tens place: The digit to the left of the ones place represents the number of tens (10¹).
- Hundreds place: The next digit to the left represents the number of hundreds (10²), and so on.
Understanding this system is crucial because it allows us to represent large numbers efficiently and perform arithmetic operations with ease. For instance, the number 345 is not simply the digits 3, 4, and 5. Instead, it represents (3 x 100) + (4 x 10) + (5 x 1), which equals 300 + 40 + 5.
Deconstructing the Problem: "7 is Ten Times the Value of What Number?"
To tackle the problem "7 is ten times the value of what number?", we must reframe it as a mathematical equation. The statement implies that if we multiply a certain number by 10, the result will be 7.
Let's represent the unknown number as x. The equation can be written as:
10 * x = 7
Our goal is to isolate x and find its value.
Methods to Solve the Problem
There are several ways to approach solving this problem, catering to different learning styles and mathematical preferences. Here are three effective methods:
1. Algebraic Method
This method involves setting up and solving a simple algebraic equation. As we established earlier, the equation is:
10 * x = 7
To solve for x, we need to perform the inverse operation of multiplication, which is division. We divide both sides of the equation by 10:
(10 * x) / 10 = 7 / 10
This simplifies to:
x = 7 / 10
x = 0.7
Therefore, the number we are looking for is 0.7.
2. Conceptual Understanding of Place Value
This method relies on a strong understanding of place value and how multiplying or dividing by 10 shifts the digits in a number.
- Multiplying by 10: When you multiply a number by 10, each digit shifts one place to the left. For example, 3 becomes 30, 45 becomes 450, and 0.2 becomes 2.
- Dividing by 10: Conversely, when you divide a number by 10, each digit shifts one place to the right. For example, 50 becomes 5, 6 becomes 0.6, and 1.8 becomes 0.18.
Applying this concept to our problem, we need to find a number that, when multiplied by 10, becomes 7. This means that 7 must be the result of shifting a digit one place to the left. To find the original number, we need to shift the 7 one place to the right.
In the number 7, the 7 is in the ones place. Shifting it one place to the right places it in the tenths place, resulting in 0.7.
3. Visual Representation: Decimal Place Value Chart
A visual representation can be particularly helpful for learners who benefit from seeing the relationship between digits and their place values. We can use a decimal place value chart to illustrate the shift.
| Place Value | Tens | Ones | . | Tenths | Hundredths |
|---|---|---|---|---|---|
| Number | 7 | . |
We want to find the number that, when multiplied by 10, equals 7. This means we need to reverse the multiplication by 10, which is division by 10.
| Place Value | Tens | Ones | . | Tenths | Hundredths |
|---|---|---|---|---|---|
| Number | 0 | . | 7 |
The chart visually demonstrates that 7 in the ones place becomes 0.7 when divided by 10, placing the 7 in the tenths place.
Why is the Answer 0.7? A Deeper Explanation
The answer 0.7 can sometimes be counterintuitive because it involves decimals. However, when we break down the value of 0.7, it becomes clearer.
- 7 represents seven-tenths, or 7/10. When we multiply 0.7 by 10, we are essentially asking, "What is ten times seven-tenths?"
Mathematically:
10 * (7/10) = (10 * 7) / 10 = 70 / 10 = 7
Alternatively, using decimals:
10 * 0.7 = 7
The multiplication by 10 shifts the decimal point one place to the right, transforming 0.7 into 7. This confirms that 7 is indeed ten times the value of 0.7.
Real-World Applications
Understanding the relationship between numbers and their place values is not just an academic exercise; it has practical applications in everyday life. Here are a few examples:
- Finance: Calculating interest rates, discounts, and percentage increases often involves multiplying or dividing by factors of 10. For example, if an item is 10% off, you need to find 1/10th (or 0.1) of the original price to determine the discount amount.
- Measurement: Converting between units, such as meters to centimeters or kilograms to grams, requires an understanding of place value. Since there are 100 centimeters in a meter, converting meters to centimeters involves multiplying by 100 (which is equivalent to shifting the decimal point two places to the right).
- Scaling Recipes: When adjusting a recipe to serve more or fewer people, you need to multiply or divide the quantities of ingredients. This often involves decimal values and requires a clear understanding of how multiplying or dividing by 10 (or other factors) affects the quantities.
- Science: In scientific calculations, especially in fields like chemistry and physics, it's common to work with very large or very small numbers. Scientific notation relies heavily on understanding place value and powers of 10.
Common Misconceptions and How to Address Them
Even with a solid understanding of place value, some misconceptions can arise when dealing with problems like "7 is ten times the value of what number?". Here are a few common misconceptions and strategies to address them:
-
Thinking the Answer Must be a Whole Number: Some students might assume that the answer must be a whole number, leading them to incorrectly guess numbers like 6 or 8.
- How to Address: Emphasize that numbers can be fractions or decimals. Provide examples of decimal numbers and their relationship to whole numbers. Show how dividing a whole number by 10 often results in a decimal.
-
Confusing Multiplication and Division: Students might mistakenly multiply 7 by 10 instead of dividing, leading to an incorrect answer of 70.
- How to Address: Reiterate the inverse relationship between multiplication and division. Explain that since 7 is the result of multiplying an unknown number by 10, we need to reverse the operation by dividing.
-
Misunderstanding Decimal Place Value: Students might struggle with the concept of tenths, hundredths, and other decimal places.
- How to Address: Use visual aids like place value charts and number lines to illustrate the value of each decimal place. Provide plenty of practice with reading and writing decimal numbers.
-
Ignoring the Importance of the Ones Place: Students may overlook the significance of the ones place as a reference point.
- How to Address: Consistently refer back to the ones place when explaining place value concepts. Highlight how each place value is related to the ones place (e.g., tens are 10 times the ones, tenths are 1/10th of the ones).
Advanced Applications and Extensions
Once the basic concept is understood, you can extend the problem to more complex scenarios to challenge students and deepen their understanding. Here are a few examples:
- Using Different Multiples: Instead of "ten times," you can use other multiples, such as "five times" or "twenty times." For example: "15 is five times the value of what number?" (Answer: 3)
- Introducing Exponents: Relate the problem to powers of 10. For instance, you could ask: "500 is ten to the power of two (10²) times what number?" (Answer: 5)
- Working with Larger Numbers: Use larger numbers to increase the complexity. For example: "7000 is ten times the value of what number?" (Answer: 700)
- Combining Operations: Incorporate additional arithmetic operations into the problem. For instance: "If you multiply a number by 10 and then add 5, you get 35. What is the number?" (Answer: 3)
- Creating Real-World Scenarios: Develop word problems that apply the concept to realistic situations. For example: "A store sells a laptop for $700. This price is ten times the cost of the tablet. How much does the tablet cost?" (Answer: $70)
The Importance of Practice and Reinforcement
As with any mathematical concept, practice is key to mastery. Provide students with ample opportunities to solve similar problems and reinforce their understanding of place value. Here are some effective strategies:
- Worksheets: Create worksheets with a variety of problems involving different multiples and numbers.
- Games: Use games to make learning fun and engaging. For example, you can create a place value bingo game or a math scavenger hunt.
- Online Resources: Utilize online resources such as interactive tutorials, practice quizzes, and educational videos.
- Group Activities: Encourage students to work together in small groups to solve problems and explain their reasoning to each other.
- Regular Review: Periodically review place value concepts to prevent forgetting and reinforce understanding.
Conclusion: Solidifying Understanding of Place Value
The question "7 is ten times the value of what number?" is more than just a simple math problem. It is a gateway to understanding the fundamental concept of place value, which is crucial for success in mathematics and its applications in real-world scenarios. By breaking down the problem, exploring different solution methods, addressing common misconceptions, and providing ample practice, educators and learners can solidify their understanding of place value and build a strong foundation for future mathematical learning. Whether through algebraic equations, conceptual explanations, or visual aids, the key is to make the concept accessible and engaging for all learners.
Latest Posts
Latest Posts
-
1 Document Your Focused Musculoskeletal Assessment Of Edith Jacobson
Nov 14, 2025
-
Absolute Advantage Is Found By Comparing Different Producers
Nov 14, 2025
-
A Firms Cost Curves Are Given In The Following Table
Nov 14, 2025
-
Ppra Gives Parents Some Level Of Control Over Their Childs
Nov 14, 2025
-
A Pregnant Client Is Admitted To The Unit For Preeclampsia
Nov 14, 2025
Related Post
Thank you for visiting our website which covers about 7 Is Ten Times The Value Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.