57 Is 95 Of What Number
planetorganic
Nov 18, 2025 · 8 min read
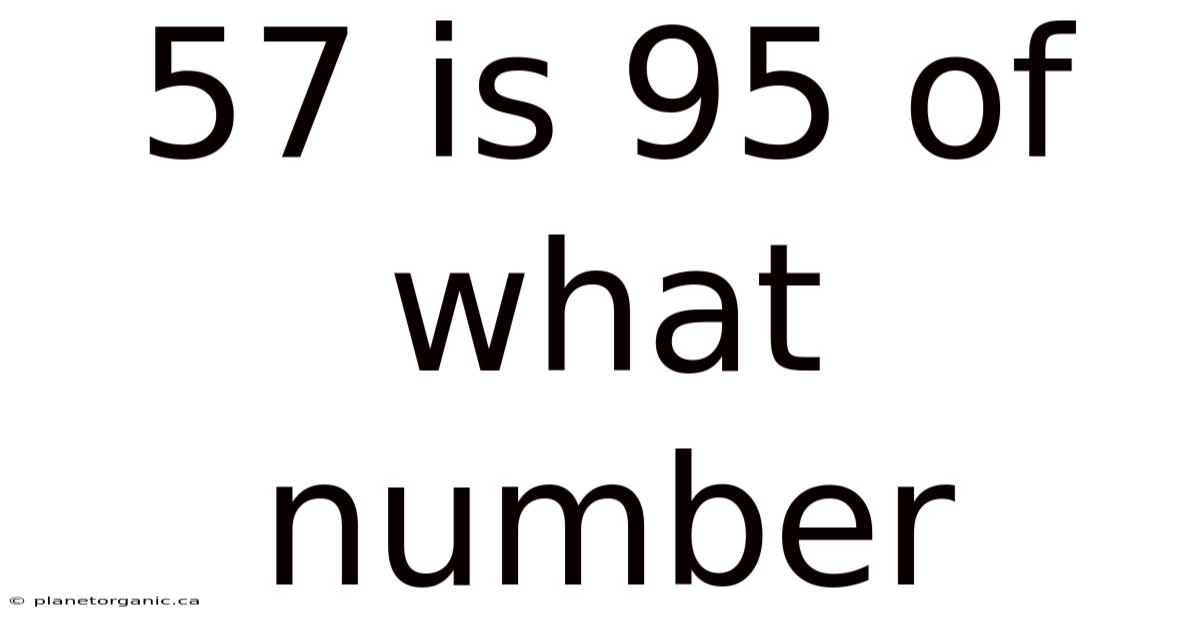
Table of Contents
Understanding percentage problems can sometimes feel like navigating a maze. But with a clear understanding of the underlying principles and a step-by-step approach, even seemingly complex questions like "57 is 95% of what number?" can be easily solved. This article will break down the problem, explain the methodology, and provide you with the tools to tackle similar percentage-based questions with confidence.
Deciphering the Percentage Puzzle
The question "57 is 95% of what number?" is a classic percentage problem. To solve it, we need to understand what each part of the statement represents mathematically. The key here is to translate the words into an equation. Let's break it down:
- "Is" often translates to an equals sign (=).
- "Of" typically indicates multiplication (x).
- "What number" represents the unknown value we are trying to find, which we can denote with a variable (e.g., x, n, or y).
Therefore, the statement "57 is 95% of what number?" can be rewritten as the following equation:
57 = 95% * x
Now, our goal is to isolate x and find its value.
Step-by-Step Solution: Finding the Unknown Number
Here’s a detailed breakdown of how to solve the equation 57 = 95% * x:
Step 1: Convert the Percentage to a Decimal
Percentages are essentially fractions out of 100. To work with percentages in equations, we need to convert them to their decimal equivalent. To do this, simply divide the percentage by 100.
In our case, we have 95%. Dividing 95 by 100 gives us 0.95.
So, our equation now becomes:
57 = 0.95 * x
Step 2: Isolate the Variable
Our next step is to isolate the variable x on one side of the equation. Since x is being multiplied by 0.95, we can isolate x by dividing both sides of the equation by 0.95. This maintains the balance of the equation.
Dividing both sides by 0.95, we get:
57 / 0.95 = (0.95 * x) / 0.95
This simplifies to:
60 = x
Step 3: Interpret the Result
We have now found the value of x, which represents the "what number" from our original problem. Therefore, 57 is 95% of 60.
Step 4: Verify the Solution (Optional)
To ensure our answer is correct, we can plug the value of x back into the original equation and see if it holds true.
We calculated x to be 60. So, let's calculate 95% of 60:
- 95 * 60 = 57
Since this matches the original statement (57 is 95% of what number?), our solution is correct.
Alternative Method: Using Proportions
Another approach to solving percentage problems is using proportions. A proportion is an equation that states that two ratios are equal. We can set up a proportion based on the information given in the problem.
Step 1: Set up the Proportion
In this case, we know that 57 represents 95% of the unknown number. We can set up the following proportion:
57 / x = 95 / 100
Here, 57 is to x as 95 is to 100.
Step 2: Cross-Multiply
To solve the proportion, we cross-multiply. This means multiplying the numerator of the first fraction by the denominator of the second fraction, and vice versa.
Cross-multiplying, we get:
57 * 100 = 95 * x
This simplifies to:
5700 = 95 * x
Step 3: Isolate the Variable
Now, we need to isolate x. Similar to the previous method, we divide both sides of the equation by 95:
5700 / 95 = (95 * x) / 95
This simplifies to:
60 = x
Step 4: Interpret the Result
As before, we find that x = 60. Therefore, 57 is 95% of 60.
This method using proportions arrives at the same answer as the decimal conversion method, providing an alternative way to solve percentage problems.
Understanding the Underlying Concepts
While we've covered the mechanics of solving the problem, it's crucial to understand the underlying concepts of percentages.
- What is a Percentage? A percentage is a way of expressing a number as a fraction of 100. The word "percent" comes from the Latin "per centum," meaning "out of one hundred." Therefore, 95% is simply 95 out of 100, or 95/100.
- Base, Rate, and Percentage: In percentage problems, there are three key components:
- Base (B): The whole amount or the original number. In our problem, this is the "what number" we're trying to find (x).
- Rate (R): The percentage being applied to the base. In our problem, this is 95%.
- Percentage (P): The portion of the base that is being considered. In our problem, this is 57.
The relationship between these three components can be expressed by the formula:
P = R * B
In our case, 57 = 0.95 * x. Understanding this formula helps in recognizing the roles of different numbers in any percentage problem.
Real-World Applications of Percentage Calculations
Percentage calculations are not just confined to textbooks; they are prevalent in everyday life. Here are a few examples:
- Discounts: When shopping, we often encounter discounts expressed as percentages. Calculating the actual discount amount involves finding a percentage of the original price. For example, a 20% discount on a $100 item means you save 20% of $100, which is $20.
- Taxes: Sales tax is often calculated as a percentage of the purchase price. To find the total cost of an item, you need to calculate the tax amount and add it to the original price.
- Interest Rates: Interest rates on loans and savings accounts are expressed as percentages. Understanding these percentages is crucial for making informed financial decisions. For example, a 5% interest rate on a savings account means you earn 5% of your balance each year.
- Statistics: Percentages are widely used in statistics to represent proportions and compare data. For example, a survey might show that 60% of respondents prefer a certain product.
- Grades: In education, grades are often expressed as percentages. A score of 85% on a test means you answered 85 out of 100 questions correctly.
The ability to confidently solve percentage problems is a valuable skill that empowers you to navigate various aspects of daily life.
Common Mistakes to Avoid
While the process of solving percentage problems is relatively straightforward, there are a few common mistakes to watch out for:
- Forgetting to Convert Percentages to Decimals: This is a crucial step. Failing to convert the percentage to a decimal before performing calculations will lead to incorrect answers. Remember to divide the percentage by 100.
- Misinterpreting the Problem: Carefully read the problem statement to understand which value represents the base, rate, and percentage. Misidentifying these values will lead to setting up the equation incorrectly.
- Incorrectly Setting up Proportions: When using proportions, ensure that the ratios are set up correctly. Make sure that corresponding values are placed in the correct positions (numerator or denominator).
- Rounding Errors: Avoid rounding intermediate calculations prematurely. Rounding should only be done at the very end to minimize potential errors.
- Not Checking Your Answer: Always take a moment to check your answer by plugging it back into the original equation or problem statement. This helps to identify any mistakes and ensures the solution is accurate.
Practice Problems to Sharpen Your Skills
To solidify your understanding of percentage problems, try solving these practice questions:
- 30 is 25% of what number?
- 120 is 80% of what number?
- 75 is 150% of what number?
- 42 is 60% of what number?
- 9 is 10% of what number?
(Answers: 1. 120, 2. 150, 3. 50, 4. 70, 5. 90)
By working through these practice problems, you'll gain confidence in your ability to solve a wide range of percentage-related questions.
Advanced Percentage Concepts
Once you've mastered the basics, you can explore more advanced percentage concepts, such as:
- Percentage Increase and Decrease: These involve calculating the percentage change between two values. The formula for percentage increase is: [(New Value - Old Value) / Old Value] * 100. The formula for percentage decrease is: [(Old Value - New Value) / Old Value] * 100.
- Compound Interest: This is a powerful concept where interest is earned not only on the principal amount but also on the accumulated interest from previous periods. The formula for compound interest is: A = P (1 + r/n)^(nt), where A is the final amount, P is the principal, r is the interest rate, n is the number of times interest is compounded per year, and t is the number of years.
- Successive Percentage Changes: These involve applying multiple percentage changes in sequence. It's important to note that successive percentage changes are not simply additive. For example, a 10% increase followed by a 10% decrease does not result in the original value.
Understanding these advanced concepts will further enhance your ability to apply percentage calculations in more complex scenarios.
The Power of Understanding Percentages
Mastering percentage calculations is more than just a mathematical skill; it's a valuable tool that empowers you to make informed decisions in various aspects of life. From understanding discounts and interest rates to analyzing statistics and tracking personal finances, percentages are an integral part of our daily experiences.
By understanding the underlying concepts, practicing regularly, and avoiding common mistakes, you can confidently solve percentage problems and leverage this skill to navigate the world around you more effectively. So, embrace the power of percentages and unlock your potential for informed decision-making!
Latest Posts
Latest Posts
-
Under The Texas Constitution Who Has The Power Of Impeachment
Nov 18, 2025
-
Product Possibilities Curve Practice Answer Key
Nov 18, 2025
-
Genetics Practice 2 Beyond The Basics
Nov 18, 2025
-
How Can The Orchestration In Wagners Operas Best Be Described
Nov 18, 2025
-
Ineffective Ventilation And A Central Pulse
Nov 18, 2025
Related Post
Thank you for visiting our website which covers about 57 Is 95 Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.