55 Of What Number Is 22
planetorganic
Nov 25, 2025 · 7 min read
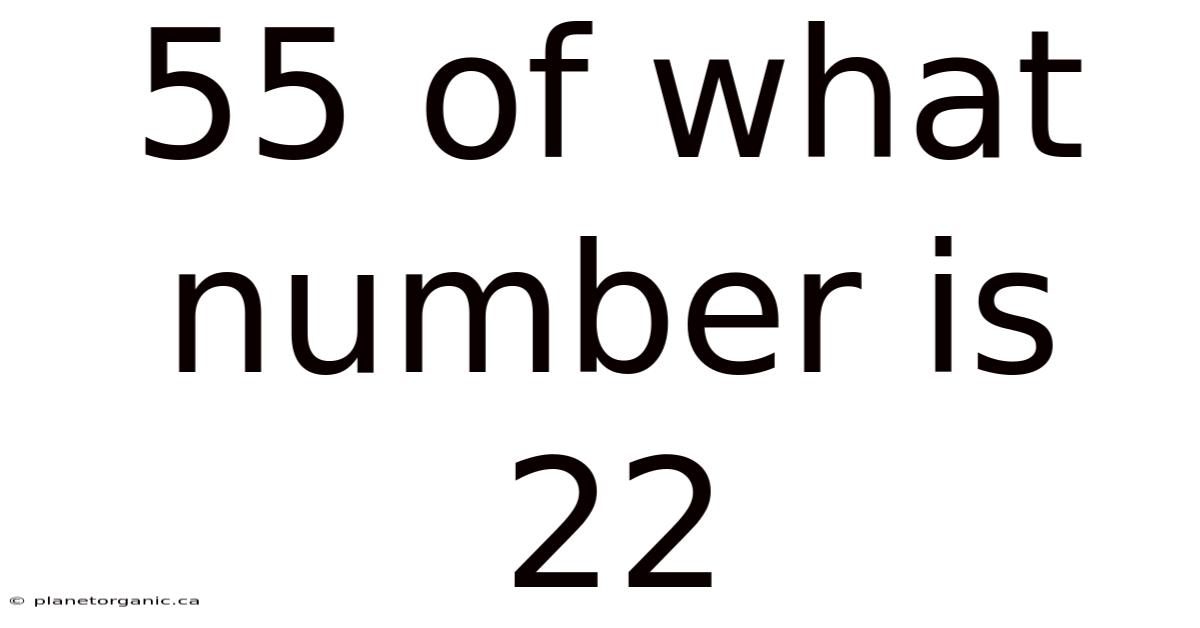
Table of Contents
Unlocking the Mystery: Finding the Number When 55% Equals 22
Percentage problems can often feel like a puzzle, but they're actually quite straightforward once you understand the underlying principles. The question "55% of what number is 22?" is a common type of percentage problem. This article will provide a comprehensive, step-by-step guide to solving this problem, along with explanations to enhance your understanding of percentages and their applications. We'll explore different approaches, delve into the mathematical concepts involved, and offer real-world examples to illustrate the power of percentage calculations.
Understanding the Basics of Percentages
Before diving into solving the problem, it's crucial to grasp the fundamental concepts of percentages. A percentage is simply a way of expressing a number as a fraction of 100. The word "percent" comes from the Latin per centum, meaning "out of one hundred." Therefore, 55% means 55 out of every 100.
Key Components:
- Percentage: The value expressed as a fraction of 100 (e.g., 55%).
- Base: The whole or total amount to which the percentage is applied (the "what number" we are trying to find).
- Amount: The portion of the base that the percentage represents (e.g., 22).
In the question "55% of what number is 22?", we know the percentage (55%) and the amount (22), and we need to find the base.
Method 1: The Equation Approach
The most direct way to solve this problem is by setting up an equation. We can translate the words into mathematical symbols:
- "55%" can be written as 0.55 (by dividing 55 by 100).
- "of" means multiplication.
- "what number" can be represented by the variable x.
- "is" means equals.
Therefore, the question "55% of what number is 22?" translates to the equation:
- 55 * x = 22
Solving for x:
To isolate x and find its value, we need to divide both sides of the equation by 0.55:
x = 22 / 0.55
x = 40
Therefore, 55% of 40 is 22.
Step-by-Step Breakdown:
- Convert the percentage to a decimal: Divide the percentage (55) by 100 to get 0.55.
- Set up the equation: 0.55 * x = 22
- Isolate the variable: Divide both sides of the equation by 0.55.
- Solve for x: x = 40
Method 2: The Proportion Method
Another way to solve percentage problems is by using proportions. A proportion is an equation that states that two ratios are equal. In this case, we can set up the following proportion:
55 / 100 = 22 / x
This proportion states that 55 is to 100 as 22 is to x.
Solving for x:
To solve for x, we can cross-multiply:
55 * x = 22 * 100
55x = 2200
Now, divide both sides by 55:
x = 2200 / 55
x = 40
Therefore, 55% of 40 is 22.
Step-by-Step Breakdown:
- Set up the proportion: 55 / 100 = 22 / x
- Cross-multiply: 55 * x = 22 * 100
- Simplify: 55x = 2200
- Isolate the variable: Divide both sides of the equation by 55.
- Solve for x: x = 40
Method 3: Using Fractions
Percentages can also be expressed as fractions. 55% is equivalent to the fraction 55/100. We can simplify this fraction to 11/20. The problem then becomes:
11/20 of what number is 22?
Let x represent the unknown number. We can set up the equation:
(11/20) * x = 22
Solving for x:
To isolate x, we multiply both sides of the equation by the reciprocal of 11/20, which is 20/11:
x = 22 * (20/11)
x = (22 * 20) / 11
x = 440 / 11
x = 40
Therefore, 55% of 40 is 22.
Step-by-Step Breakdown:
- Convert the percentage to a fraction: 55% = 55/100 = 11/20
- Set up the equation: (11/20) * x = 22
- Multiply by the reciprocal: Multiply both sides of the equation by 20/11.
- Simplify: x = (22 * 20) / 11
- Solve for x: x = 40
Real-World Applications of Percentage Calculations
Percentage calculations are used extensively in everyday life. Understanding how to solve problems like "55% of what number is 22?" is crucial for making informed decisions in various situations. Here are a few examples:
- Discounts: Imagine a store is offering a 55% discount on an item, and you save $22. What was the original price of the item? This is the same problem, and the original price would be $40.
- Sales Commissions: A salesperson earns a 55% commission on a sale, and their commission is $22. What was the total value of the sale? Again, the sale was worth $40.
- Test Scores: If you answered 55% of the questions correctly on a test and got 22 questions right, how many questions were on the test in total? The test had 40 questions.
- Ingredients in a Recipe: A recipe requires that 55% of the liquid be water, and the amount of water needed is 22 ounces. How much total liquid is needed? You would need a total of 40 ounces of liquid.
- Financial Investments: You have invested in a stock and it has grown by 55%, resulting in a gain of $22. What was your initial investment? Your initial investment was $40.
Common Mistakes to Avoid
While the concepts are relatively simple, there are a few common mistakes people make when solving percentage problems:
- Incorrectly converting percentages to decimals: Remember to divide the percentage by 100 to get the decimal equivalent. For example, 55% is 0.55, not 5.5.
- Misinterpreting the question: Make sure you understand what the problem is asking. Are you trying to find the percentage, the base, or the amount?
- Setting up the equation incorrectly: Pay close attention to the wording of the problem and translate it accurately into a mathematical equation.
- Arithmetic errors: Double-check your calculations to avoid simple mistakes.
Advanced Percentage Concepts
Once you've mastered the basics, you can explore more advanced percentage concepts, such as:
- Percentage Increase and Decrease: Calculating the percentage change between two values.
- Compound Interest: Calculating interest earned on both the principal and accumulated interest.
- Weighted Averages: Calculating an average where different values have different weights or importance.
- Successive Percentages: Applying multiple percentage changes in a sequence. For instance, understanding how multiple discounts affect the final price of an item.
- Reverse Percentage Problems: These involve working backward to find an original value after a percentage increase or decrease has been applied.
Tips for Mastering Percentage Problems
- Practice Regularly: The more you practice, the more comfortable you will become with solving percentage problems.
- Understand the Concepts: Don't just memorize formulas; make sure you understand the underlying principles.
- Break Down Complex Problems: Divide complex problems into smaller, more manageable steps.
- Use Real-World Examples: Relate percentage problems to real-world situations to make them more meaningful.
- Check Your Answers: Always check your answers to make sure they are reasonable and accurate.
- Draw Diagrams: Visual aids can sometimes help in understanding the relationships between different values.
- Use Estimation: Before solving, estimate the answer to get a sense of what the result should be.
Solving More Complex Problems
Let's look at a slightly more complex problem to further illustrate the concepts:
"If 15% of a number is 30, what is 60% of that same number?"
First, we need to find the original number. We know that:
- 15 * x = 30
Solving for x:
x = 30 / 0.15
x = 200
Now that we know the original number is 200, we can find 60% of it:
- 60 * 200 = 120
So, 60% of the number is 120. This shows how solving one percentage problem can be a stepping stone to solving another related problem.
Conclusion
Understanding percentages is a fundamental skill that is essential for success in many areas of life. By mastering the concepts and practicing regularly, you can become confident in your ability to solve percentage problems of all kinds. Whether you're calculating discounts, understanding financial statements, or analyzing data, a solid understanding of percentages will serve you well. The question "55% of what number is 22?" is just one example of the many practical applications of percentage calculations. By using the methods described in this article, you can confidently solve this type of problem and apply your knowledge to a wide range of real-world situations.
Latest Posts
Latest Posts
-
1 2 Cup Heavy Cream Calories
Nov 25, 2025
-
Amoeba Sisters Video Recap Nature Of Science
Nov 25, 2025
-
The Fixed Cost Per Unit Is Equal To
Nov 25, 2025
-
Ap Biology Unit 7 Progress Check Mcq Part B
Nov 25, 2025
-
He Wishes For The Cloths Of Heaven
Nov 25, 2025
Related Post
Thank you for visiting our website which covers about 55 Of What Number Is 22 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.