51 Is 85 Of What Number
planetorganic
Nov 14, 2025 · 6 min read
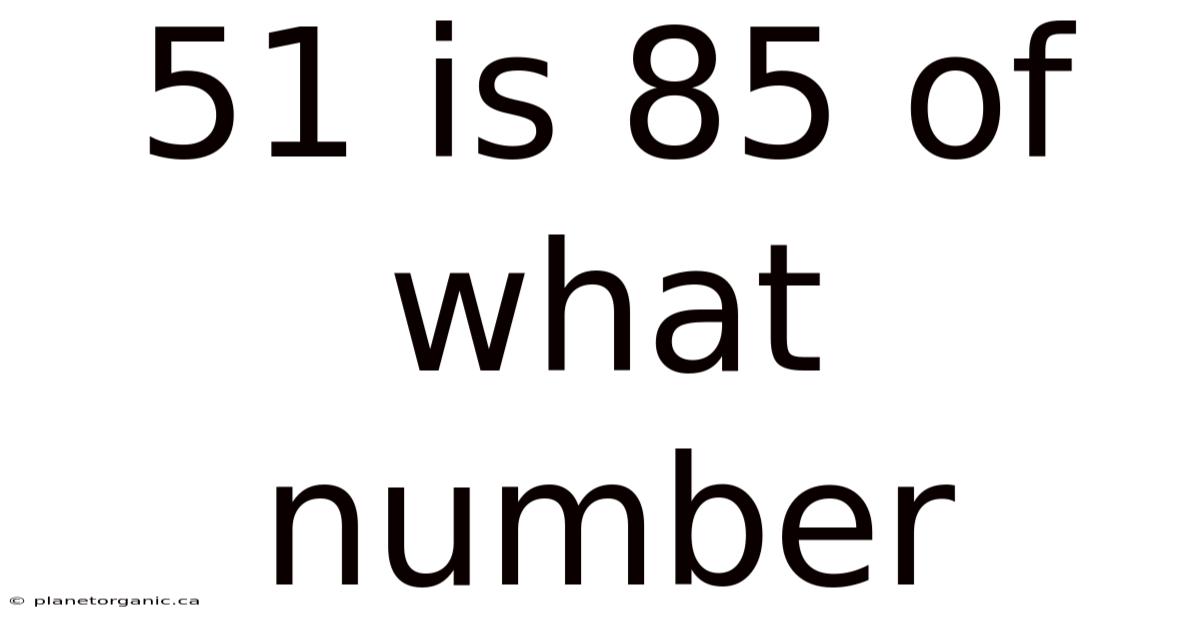
Table of Contents
Unlocking the Puzzle: Decoding "51 is 85% of What Number?"
At first glance, the question "51 is 85% of what number?" might seem like a simple math problem. However, it embodies a fundamental concept of percentages and their application in everyday scenarios. Understanding how to solve this type of problem is crucial for various situations, from calculating discounts to analyzing financial data. Let's embark on a journey to dissect this question, explore different solution methods, and delve into the underlying principles that make it all click.
Understanding Percentages: A Foundation
Before diving into the specifics of the problem, let's solidify our understanding of percentages. A percentage is essentially a fraction or ratio expressed as a portion of 100. The word "percent" comes from the Latin "per centum," meaning "out of one hundred." So, 85% simply means 85 out of every 100.
-
Representing Percentages: Percentages can be represented in three main forms:
- Percentage Form: This is the most common form, using the "%" symbol (e.g., 85%).
- Decimal Form: To convert a percentage to a decimal, divide it by 100 (e.g., 85% = 85/100 = 0.85).
- Fraction Form: Percentages can also be expressed as fractions (e.g., 85% = 85/100 = 17/20).
-
The Importance of the "Of": In percentage problems, the word "of" is often used to indicate multiplication. For example, "85% of a number" means 85% multiplied by that number.
Decoding the Question: "51 is 85% of What Number?"
Now, let's break down the question: "51 is 85% of what number?" This sentence implies that 51 represents a portion (85%) of an unknown whole number. Our goal is to find that whole number.
Here's how we can translate the sentence into a mathematical equation:
- Let "x" represent the unknown number.
- "Is" translates to "=".
- "85%" translates to 0.85 (in decimal form).
- "Of" translates to multiplication (*).
Therefore, the equation becomes: 51 = 0.85 * x
Method 1: The Algebraic Approach
The algebraic approach involves using the equation we derived above to solve for the unknown variable, "x."
-
The Equation: As we established, the equation is 51 = 0.85 * x
-
Isolating "x": To find the value of "x," we need to isolate it on one side of the equation. We can do this by dividing both sides of the equation by 0.85:
- 51 / 0.85 = (0.85 * x) / 0.85
-
Simplifying: This simplifies to:
- 60 = x
-
The Answer: Therefore, the unknown number "x" is 60. So, 51 is 85% of 60.
Method 2: The Proportion Method
The proportion method relies on the concept of equivalent ratios. We can set up a proportion to represent the relationship between the percentage, the part, and the whole.
-
Setting Up the Proportion: We know that 51 is 85% of the unknown number. We can express this as a proportion:
-
51 / x = 85 / 100
-
Where:
- 51 represents the part (the value that is a percentage of the whole).
- x represents the whole (the unknown number we are trying to find).
- 85 represents the percentage.
- 100 represents the total (100% of the whole).
-
-
Cross-Multiplication: To solve the proportion, we cross-multiply:
- 51 * 100 = 85 * x
-
Simplifying: This gives us:
- 5100 = 85x
-
Isolating "x": Now, we divide both sides by 85 to isolate "x":
- 5100 / 85 = 85x / 85
-
The Answer: This simplifies to:
- 60 = x
-
Conclusion: Again, we find that the unknown number "x" is 60.
Method 3: The Unitary Method
The unitary method involves finding the value of one unit (1%) and then using that value to find the value of the whole (100%).
-
Finding the Value of 1%: We know that 85% is equal to 51. To find the value of 1%, we divide 51 by 85:
- 1% = 51 / 85 = 0.6
-
Finding the Value of 100%: Now that we know the value of 1%, we can find the value of 100% by multiplying 0.6 by 100:
- 100% = 0.6 * 100 = 60
-
The Answer: Therefore, 51 is 85% of 60.
Practical Applications: Where This Knowledge Matters
Understanding how to solve percentage problems like "51 is 85% of what number?" extends beyond the realm of theoretical mathematics. It has practical applications in various real-world scenarios:
-
Sales and Discounts: Imagine you're buying a shirt that's on sale for 15% off, and the discounted price is $51. You can use this method to calculate the original price of the shirt.
-
Financial Analysis: In finance, you might need to determine the original value of an investment based on its current value and the percentage growth or loss.
-
Calculating Taxes: Understanding percentages is crucial for calculating sales tax, income tax, and property tax.
-
Data Analysis: In data analysis, you might need to calculate the total number of respondents in a survey based on the number of respondents who answered a certain way and the percentage that represents.
-
Calculating Tips: Although not directly related to the "51 is 85% of what number?" question, understanding percentages is essential for calculating tips at restaurants.
Common Mistakes to Avoid
While solving percentage problems, it's crucial to avoid common mistakes that can lead to incorrect answers:
-
Confusing the Part and the Whole: Always carefully identify which value represents the part (the percentage of the whole) and which represents the whole (the unknown number).
-
Incorrectly Converting Percentages: Make sure to correctly convert percentages to decimals or fractions before performing calculations. Forgetting to divide by 100 is a common error.
-
Misinterpreting the Question: Read the question carefully to understand what you're being asked to find. Sometimes, the wording can be tricky.
-
Rounding Errors: Avoid rounding intermediate values during calculations, as this can lead to inaccuracies in the final answer. Round only at the very end, if necessary.
Enhancing Your Understanding: Practice Problems
To solidify your understanding of percentage problems, try solving the following practice problems:
- Problem: 36 is 45% of what number?
- Problem: 120 is 75% of what number?
- Problem: 25 is 20% of what number?
- Problem: A store is having a 30% off sale. If an item costs $42 after the discount, what was the original price?
- Problem: A student scored 80% on a test and got 40 questions correct. How many questions were on the test in total?
Beyond the Basics: Exploring More Complex Percentage Problems
Once you've mastered the basics, you can explore more complex percentage problems that involve multiple steps or require a deeper understanding of the concepts. Here are some examples:
-
Percentage Increase and Decrease: Problems involving percentage increase or decrease require you to calculate the change in value as a percentage of the original value.
-
Compound Interest: Compound interest involves calculating interest on both the principal amount and the accumulated interest.
-
Mixture Problems: Mixture problems involve combining different solutions with varying concentrations to achieve a desired concentration.
-
Reverse Percentage Problems: These problems require you to find the original value after a series of percentage changes.
Conclusion: The Power of Percentages
The question "51 is 85% of what number?" might seem simple, but it highlights the importance of understanding percentages and their applications. By mastering the different methods for solving percentage problems and avoiding common mistakes, you can unlock a powerful tool for analyzing data, making informed decisions, and navigating various real-world scenarios. Percentages are more than just numbers; they are a fundamental language for understanding proportions and relationships in the world around us. Embrace the power of percentages, and you'll be well-equipped to tackle a wide range of challenges in mathematics, finance, and beyond.
Latest Posts
Latest Posts
-
Which Ics Functional Area Arranges For Resources
Nov 14, 2025
-
Who Makes The Decisions In A Command Economy
Nov 14, 2025
-
What Is The Multiplication Symbol In Excel
Nov 14, 2025
-
Ap Precalculus Mixed Six Topics 1 1 1 3 Rates Of Change
Nov 14, 2025
-
Worse Than Slavery Cartoon Questions And Answers
Nov 14, 2025
Related Post
Thank you for visiting our website which covers about 51 Is 85 Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.