50 Out Of 70 As A Percentage
planetorganic
Nov 17, 2025 · 7 min read
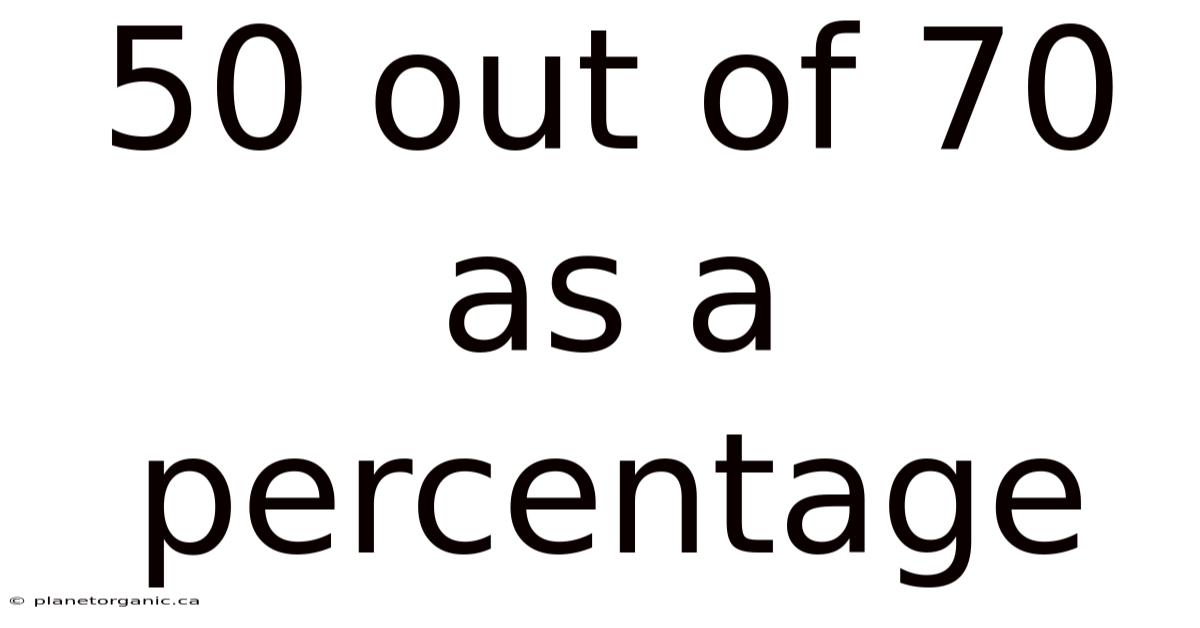
Table of Contents
Calculating percentages is a fundamental skill applicable in various aspects of life, from understanding academic scores to analyzing financial data. Understanding how to convert fractions to percentages is not only useful for students but also for professionals who deal with statistics and data analysis regularly. Let's delve into the straightforward process of calculating what percentage 50 is out of 70, providing clear steps and explanations to ensure comprehension.
Understanding the Basics of Percentages
Before we dive into the calculation, let’s define what a percentage is. A percentage is a way of expressing a number as a fraction of 100. The word "percent" comes from the Latin "per centum," meaning "out of one hundred." Therefore, when we say "x percent," we mean x out of 100. Percentages are used to express how large one quantity is relative to another quantity. To calculate a percentage, we generally use the following formula:
Percentage = (Part / Whole) * 100
Where:
- Part is the specific quantity you are interested in.
- Whole is the total quantity or the reference value.
Step-by-Step Calculation: 50 out of 70 as a Percentage
Now, let’s apply this formula to calculate what percentage 50 is out of 70.
Step 1: Identify the 'Part' and the 'Whole'
In this scenario:
- Part = 50
- Whole = 70
Step 2: Set up the Fraction
First, express the problem as a fraction:
Fraction = Part / Whole = 50 / 70
Step 3: Simplify the Fraction (Optional)
Simplifying the fraction can make the subsequent calculation easier. Both 50 and 70 are divisible by 10, so we can simplify the fraction:
Simplified Fraction = 50 ÷ 10 / 70 ÷ 10 = 5 / 7
Step 4: Convert the Fraction to a Decimal
To convert the fraction to a decimal, divide the numerator (the top number) by the denominator (the bottom number):
Decimal = 5 / 7 ≈ 0.7142857
(I’ve used a calculator to get a more precise decimal value. When doing calculations by hand, you might round off to a fewer number of decimal places.)
Step 5: Convert the Decimal to a Percentage
To convert the decimal to a percentage, multiply the decimal by 100:
Percentage = Decimal * 100 = 0.7142857 * 100 = 71.42857%
Step 6: Rounding the Percentage (if necessary)
In many cases, it’s practical to round the percentage to a more manageable number. Depending on the context, you might round to the nearest whole number, one decimal place, or two decimal places.
- Rounded to the nearest whole number: 71%
- Rounded to one decimal place: 71.4%
- Rounded to two decimal places: 71.43%
So, 50 out of 70 is approximately 71.43%.
Practical Examples and Applications
Understanding how to calculate percentages is useful in a variety of real-world scenarios. Here are a few examples:
1. Academic Grading
In academic settings, percentages are commonly used to represent a student's performance. For instance, if a student scores 50 out of 70 on a test, their score would be approximately 71.43%. This allows students and teachers to quickly understand the student's performance relative to the total possible score.
2. Sales and Discounts
Retailers often use percentages to denote discounts. For example, a store might offer a 30% discount on an item. If the original price of the item is $70, the discount amount can be calculated as follows:
Discount Amount = (Discount Percentage / 100) * Original Price
Discount Amount = (30 / 100) * $70 = $21
The sale price would then be $70 - $21 = $49.
3. Financial Analysis
In finance, percentages are used to analyze changes in stock prices, interest rates, and other financial metrics. For example, if an investment increases from $50 to $70, the percentage increase can be calculated as:
Percentage Increase = ((New Value - Old Value) / Old Value) * 100
Percentage Increase = (($70 - $50) / $50) * 100
Percentage Increase = ($20 / $50) * 100 = 40%
This indicates a 40% increase in the value of the investment.
4. Data Analysis
Percentages are frequently used in data analysis to represent the proportion of different categories within a dataset. For example, if you survey 70 people and find that 50 of them prefer a certain product, you can say that approximately 71.43% of the respondents prefer that product.
5. Health and Nutrition
Percentages are also used to understand nutritional information. For example, if a food item contains 50 grams of fat and the recommended daily intake is 70 grams, you can calculate the percentage of the daily value that the food item represents:
Percentage of Daily Value = (Amount of Nutrient / Recommended Daily Intake) * 100
Percentage of Daily Value = (50 / 70) * 100 ≈ 71.43%
This helps individuals make informed decisions about their diet.
Common Mistakes to Avoid
When calculating percentages, it’s easy to make mistakes. Here are some common errors to watch out for:
-
Incorrectly Identifying the 'Part' and 'Whole':
- Always ensure that you correctly identify which value is the part and which is the whole. Confusing these can lead to significant errors in your calculations.
-
Forgetting to Multiply by 100:
- One of the most common mistakes is forgetting to multiply the decimal by 100 to convert it to a percentage. Remember, a percentage is a fraction out of 100, so this step is crucial.
-
Rounding Errors:
- Be mindful of when and how you round numbers. Rounding too early in the calculation can lead to inaccuracies in the final percentage. It’s generally best to perform the calculation to several decimal places and then round the final result.
-
Misinterpreting the Context:
- Understand the context of the problem. For example, when calculating percentage increase or decrease, make sure you use the correct base value in your calculation.
Advanced Tips for Percentage Calculations
Using a Calculator
While it’s important to understand the underlying principles of percentage calculations, using a calculator can save time and reduce the likelihood of errors, especially when dealing with complex numbers. Most calculators have a percentage function that can simplify the process.
Using Spreadsheet Software
Spreadsheet software like Microsoft Excel or Google Sheets can be incredibly useful for performing percentage calculations, especially when dealing with large datasets. Here’s how you can calculate the percentage of 50 out of 70 in Excel:
-
Enter the values:
- In cell A1, enter 50.
- In cell B1, enter 70.
-
Calculate the percentage:
- In cell C1, enter the formula
=A1/B1.
- In cell C1, enter the formula
-
Format as a percentage:
- Select cell C1, go to the "Home" tab, and click the percentage (%) button in the "Number" group. You can also adjust the number of decimal places displayed.
Mental Math Techniques
Being able to perform percentage calculations mentally can be very useful in everyday situations. Here are a few techniques to improve your mental math skills:
-
Breaking Down Percentages:
- Break down the percentage into smaller, more manageable parts. For example, to calculate 15% of a number, you can calculate 10% and 5% separately and then add them together.
-
Using Benchmarks:
- Use benchmark percentages like 10%, 25%, and 50% as reference points. For example, 10% of a number is simply the number divided by 10.
-
Estimating:
- Practice estimating percentages. This can help you quickly assess whether your calculations are in the right ballpark.
Complex Percentage Problems
Sometimes, you might encounter more complex percentage problems. Here are a couple of examples:
Example 1: Finding the Original Value
If 50 represents 20% of a certain value, what is the original value?
Part = 50
Percentage = 20%
Original Value = Part / (Percentage / 100)
Original Value = 50 / (20 / 100)
Original Value = 50 / 0.2
Original Value = 250
So, the original value is 250.
Example 2: Percentage Change
A price increases from $50 to $70. What is the percentage increase?
Original Price = $50
New Price = $70
Increase = New Price - Original Price = $70 - $50 = $20
Percentage Increase = (Increase / Original Price) * 100
Percentage Increase = ($20 / $50) * 100
Percentage Increase = 0.4 * 100 = 40%
The percentage increase is 40%.
Conclusion
Calculating percentages is a versatile skill with wide-ranging applications. By understanding the basic formula and practicing regularly, you can confidently tackle percentage problems in various contexts. Remember to identify the 'part' and the 'whole' accurately, convert the fraction to a decimal, and then multiply by 100 to get the percentage. Whether you're a student, professional, or simply managing your personal finances, mastering percentage calculations will undoubtedly prove valuable.
Latest Posts
Related Post
Thank you for visiting our website which covers about 50 Out Of 70 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.