21 Is 35 Of What Number
planetorganic
Nov 25, 2025 · 8 min read
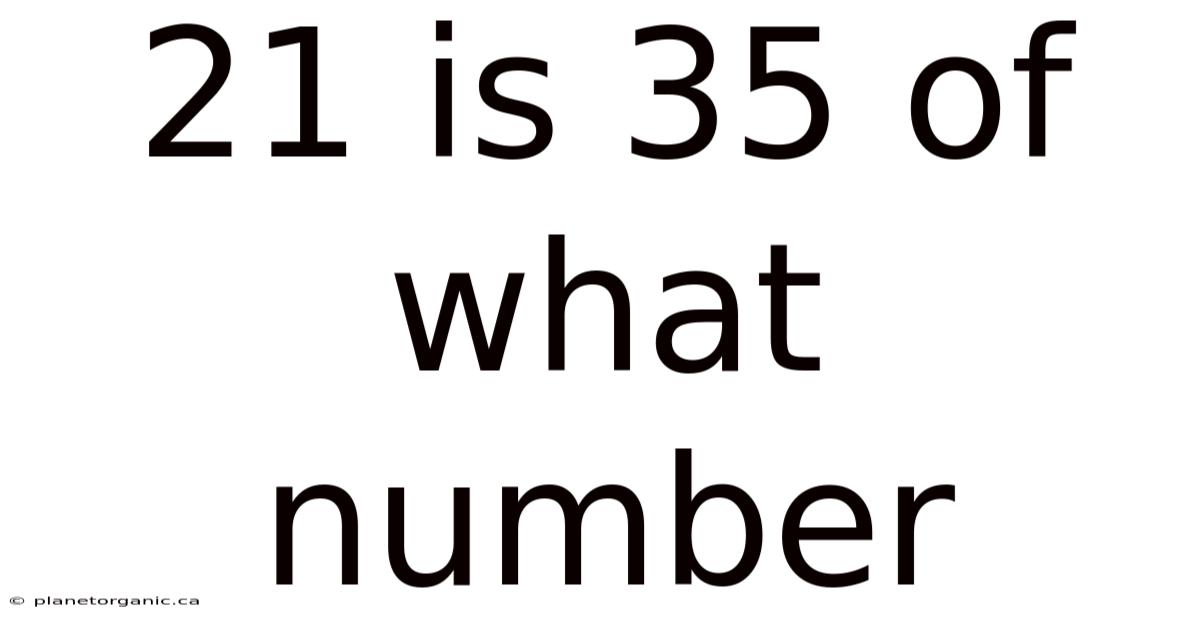
Table of Contents
Understanding percentage problems unlocks a powerful tool for everyday calculations, from calculating discounts to understanding statistics. The question "21 is 35% of what number?" falls into this category, challenging us to find the whole when we know a part and the percentage it represents. This article will provide a comprehensive, step-by-step guide on solving this type of problem, exploring the underlying concepts, and offering various methods for finding the answer. By mastering these techniques, you'll be equipped to tackle similar percentage-related questions with confidence.
Understanding the Percentage Concept
At its core, a percentage is a way of expressing a number as a fraction of 100. The word "percent" comes from the Latin per centum, meaning "out of one hundred". Therefore, 35% simply means 35 out of every 100. Understanding this basic definition is crucial for solving percentage problems. It allows us to translate percentages into fractions or decimals, which are easier to work with in mathematical calculations.
Key Terms
Before diving into the solution, let's define some key terms:
- Percentage: A ratio expressed as a fraction of 100.
- Part: The portion of the whole that is being considered (in this case, 21).
- Whole: The total or original amount that we are trying to find.
- Rate: The percentage applied to the whole to find the part (in this case, 35%).
Translating Words into Math
The key to solving word problems lies in translating the words into mathematical expressions. The phrase "21 is 35% of what number?" can be translated as follows:
- "Is" means equals (=)
- "Of" means multiply (x)
- "What number" represents the unknown variable (let's use 'x')
Therefore, the problem can be written as the equation: 21 = 0.35 * x
Method 1: Using the Percentage Formula
The most straightforward method for solving percentage problems is using the percentage formula:
Part = Rate x Whole
In our case, we know the Part (21) and the Rate (35%), and we want to find the Whole (x). We can rearrange the formula to solve for the Whole:
Whole = Part / Rate
Step-by-Step Solution
-
Convert the percentage to a decimal: Divide 35% by 100 to get 0.35.
-
Apply the formula: Substitute the known values into the formula:
x = 21 / 0.35
-
Calculate the result: Divide 21 by 0.35.
x = 60
Therefore, 21 is 35% of 60.
Method 2: Using Proportions
Another effective method involves setting up a proportion. A proportion is an equation stating that two ratios are equal. In percentage problems, we can set up a proportion relating the part to the whole and the percentage to 100.
Setting up the Proportion
We can set up the following proportion:
Part / Whole = Percentage / 100
In our problem, this translates to:
21 / x = 35 / 100
Solving the Proportion
To solve for x, we can use cross-multiplication:
-
Cross-multiply: Multiply the numerator of the first fraction by the denominator of the second fraction, and vice versa.
21 * 100 = 35 * x
-
Simplify:
2100 = 35x
-
Solve for x: Divide both sides of the equation by 35.
x = 2100 / 35
x = 60
Again, we find that 21 is 35% of 60.
Method 3: Using Algebraic Equations
This method utilizes algebraic principles to isolate the unknown variable. As we mentioned earlier, the problem "21 is 35% of what number?" can be directly translated into an algebraic equation.
Forming the Equation
Let 'x' represent the unknown number. The equation becomes:
21 = 0.35x
Solving the Equation
-
Isolate x: To isolate x, divide both sides of the equation by 0.35.
21 / 0.35 = 0.35x / 0.35
-
Simplify:
x = 60
This method confirms that 21 is 35% of 60.
Method 4: Using a Calculator
Calculators provide a quick and efficient way to solve percentage problems. Most calculators have a percentage function that simplifies the calculation.
Steps to Use a Calculator
-
Convert the percentage to a decimal: Divide 35 by 100 to get 0.35.
-
Divide the part by the decimal: Enter 21 / 0.35 into the calculator.
-
Press the equals button: The calculator will display the answer, which is 60.
This method is particularly useful for complex calculations or when speed is a priority.
Verification
Regardless of the method used, it's always a good idea to verify your answer. To do this, calculate 35% of 60 and see if it equals 21.
Calculation
-
Convert the percentage to a decimal: 35% = 0.35
-
Multiply the decimal by the whole: 0.35 * 60 = 21
Since 35% of 60 is indeed 21, our answer is correct.
Real-World Applications
Understanding how to solve percentage problems has numerous practical applications in everyday life. Here are a few examples:
-
Discounts and Sales: Calculating the final price after a discount. For example, if an item is 20% off and originally costs $80, you can calculate the discount amount and the final price.
-
Taxes: Determining the amount of sales tax on a purchase. If the sales tax rate is 6% and you buy something for $50, you can calculate the tax amount.
-
Tips: Calculating the amount to tip at a restaurant. If you want to tip 15% on a $40 bill, you can easily calculate the tip amount.
-
Financial Planning: Understanding interest rates on loans and investments. Being able to calculate percentage increases and decreases is crucial for managing finances.
-
Statistics and Data Analysis: Interpreting data presented as percentages. Understanding percentages helps in analyzing surveys, polls, and other statistical information.
-
Cooking: Adjusting recipes based on percentages. If you want to double a recipe, you need to increase the ingredients by 100%.
Common Mistakes to Avoid
While solving percentage problems, it's important to avoid common mistakes that can lead to incorrect answers. Here are some pitfalls to watch out for:
-
Forgetting to convert the percentage to a decimal: Always remember to divide the percentage by 100 before using it in calculations. Failing to do so will result in a significantly incorrect answer.
-
Misinterpreting the problem: Carefully read the problem and identify the part, the whole, and the percentage. Confusing these elements can lead to setting up the equation incorrectly.
-
Incorrectly setting up proportions: Ensure that the proportion is set up correctly, with the corresponding values in the correct positions. For example, the part should be over the whole, and the percentage should be over 100.
-
Rounding errors: Avoid rounding off numbers prematurely, as this can introduce errors in the final answer. Keep as many decimal places as possible until the final calculation.
-
Not verifying the answer: Always verify your answer to ensure that it is reasonable and accurate. This can help catch any mistakes made during the calculation process.
Advanced Percentage Problems
Once you've mastered the basics, you can tackle more complex percentage problems. These problems may involve multiple steps or require a deeper understanding of percentage concepts. Here are some examples:
-
Percentage Increase and Decrease: Calculating the percentage change between two values. The formula for percentage increase is [(New Value - Original Value) / Original Value] x 100. The formula for percentage decrease is [(Original Value - New Value) / Original Value] x 100.
-
Successive Percentages: Applying multiple percentages to a value. For example, if an item is discounted by 20% and then an additional 10%, you need to calculate the discounts sequentially, not simply add the percentages together.
-
Reverse Percentage Problems: Finding the original value after a percentage increase or decrease. For example, if a price increased by 15% to $230, you need to work backward to find the original price.
-
Mixture Problems: Calculating the percentage of a substance in a mixture. These problems often involve combining different quantities with different concentrations.
Tips for Mastering Percentage Problems
To improve your skills in solving percentage problems, consider the following tips:
-
Practice Regularly: The more you practice, the more comfortable you'll become with the different types of percentage problems and the various methods for solving them.
-
Understand the Concepts: Don't just memorize formulas; focus on understanding the underlying concepts of percentages. This will enable you to solve problems more effectively and apply your knowledge to real-world situations.
-
Break Down Complex Problems: When faced with a complex problem, break it down into smaller, more manageable steps. This will make the problem less daunting and easier to solve.
-
Use Visual Aids: Visual aids, such as diagrams and charts, can help you understand and solve percentage problems. These tools can make it easier to visualize the relationships between the part, the whole, and the percentage.
-
Seek Help When Needed: Don't hesitate to ask for help from teachers, tutors, or online resources if you're struggling with percentage problems. Getting clarification and guidance can help you overcome challenges and improve your understanding.
Conclusion
The question "21 is 35% of what number?" provides a clear and concise example of a common percentage problem. By understanding the fundamental concepts of percentages and utilizing various methods such as the percentage formula, proportions, and algebraic equations, we can confidently solve this type of problem. Remember to convert percentages to decimals, avoid common mistakes, and verify your answers to ensure accuracy. With practice and a solid understanding of the underlying principles, you can master percentage problems and apply your knowledge to a wide range of real-world scenarios. Whether you're calculating discounts, managing finances, or analyzing data, a strong grasp of percentages is an invaluable skill.
Latest Posts
Latest Posts
-
Which Statement Below Correctly Describes Merchandise Inventory
Nov 25, 2025
-
Skills Module 3 0 Vital Signs Posttest
Nov 25, 2025
-
Skills Module 3 0 Blood Administration Pretest
Nov 25, 2025
-
A Hospice Nurse Is Caring For A Client
Nov 25, 2025
-
Test Bank For Nursing Medical Surgical
Nov 25, 2025
Related Post
Thank you for visiting our website which covers about 21 Is 35 Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.