1.23 1 Lab Divide By X
planetorganic
Nov 15, 2025 · 9 min read
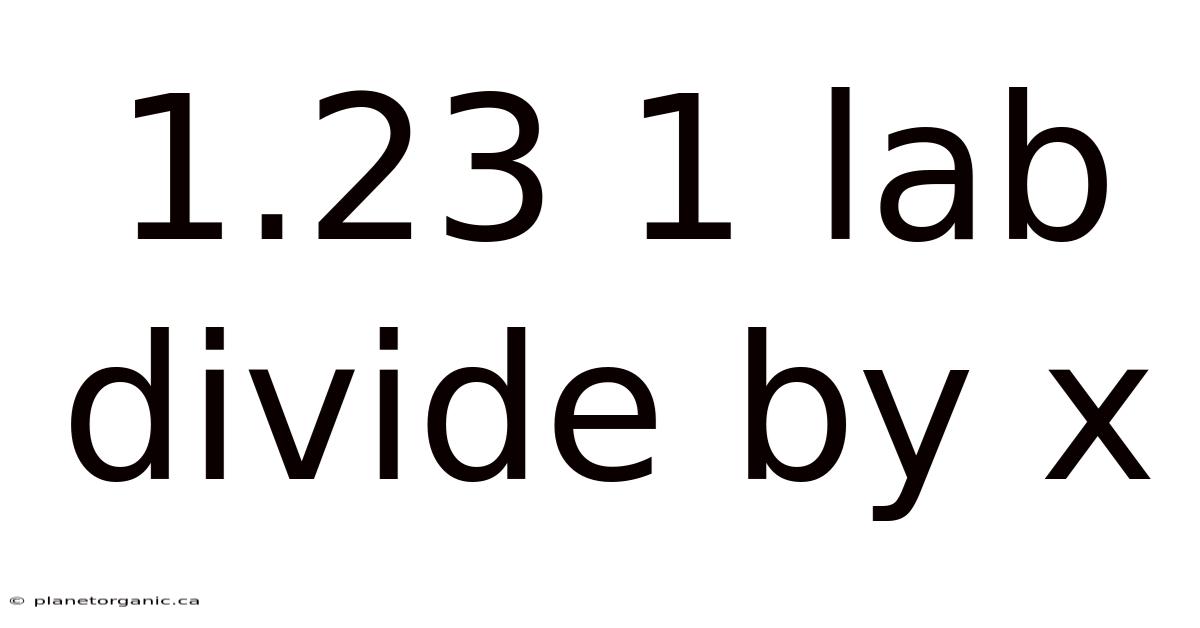
Table of Contents
Unraveling 1.23 ÷ x: A Comprehensive Guide to Division with Variables
Division is a fundamental arithmetic operation, and understanding how to perform it, especially when variables are involved, is crucial for success in algebra and beyond. This article will explore the expression 1.23 ÷ x, dissecting its meaning, exploring different scenarios, and providing a clear understanding of how to work with this type of expression. We will delve into practical applications, potential pitfalls, and strategies for simplifying and solving equations involving this division.
Understanding the Expression 1.23 ÷ x
The expression "1.23 ÷ x" represents the division of the number 1.23 by the variable 'x'. In mathematical terms, 'x' represents an unknown value. This expression can also be written as a fraction: 1.23/x. The goal is often to determine the value of the expression for a given value of x, or to solve for 'x' if the expression is part of an equation.
- 1.23: This is the dividend, the number being divided. It's a constant, meaning its value is fixed.
- x: This is the divisor, the number we are dividing by. It's a variable, meaning its value can change.
- ÷: This symbol represents the division operation. It's often replaced by a fraction bar (/).
The value of the expression 1.23 ÷ x depends entirely on the value assigned to the variable 'x'.
Scenarios and Examples: Calculating 1.23 ÷ x for Different Values of x
Let's explore how the value of 1.23 ÷ x changes with different values of 'x':
- If x = 1: 1.23 ÷ 1 = 1.23. Dividing any number by 1 results in the number itself.
- If x = 2: 1.23 ÷ 2 = 0.615. We are essentially halving 1.23.
- If x = 0.5: 1.23 ÷ 0.5 = 2.46. Dividing by a number less than 1 results in a larger quotient. This is the same as multiplying 1.23 by 2.
- If x = 0.1: 1.23 ÷ 0.1 = 12.3. Notice how dividing by a smaller decimal increases the result significantly.
- If x = 10: 1.23 ÷ 10 = 0.123. Dividing by 10 shifts the decimal point one place to the left.
- If x = 100: 1.23 ÷ 100 = 0.0123. Dividing by 100 shifts the decimal point two places to the left.
- If x = 1.23: 1.23 ÷ 1.23 = 1. Dividing a number by itself always equals 1 (except when the number is 0).
- If x = -1: 1.23 ÷ -1 = -1.23. Dividing a positive number by a negative number results in a negative quotient.
- If x = -2: 1.23 ÷ -2 = -0.615. Again, the result is negative.
These examples highlight the inverse relationship between 'x' and the value of the expression 1.23 ÷ x. As 'x' increases, the value of the expression decreases, and vice versa. The sign of 'x' also determines the sign of the result.
The Critical Case: x = 0
Division by zero is undefined in mathematics. This is a fundamental rule. Therefore, the expression 1.23 ÷ x is undefined when x = 0. Think of it this way: division asks the question, "How many times does the divisor fit into the dividend?" If the divisor is zero, it cannot "fit" into any number, including 1.23.
Mathematically, we represent this as:
1.23 ÷ 0 = Undefined
Attempting to perform this calculation on a calculator will usually result in an error message. This is because the operation is mathematically invalid.
Solving Equations Involving 1.23 ÷ x
The expression 1.23 ÷ x often appears in equations that need to be solved for 'x'. Here's how to approach different types of equations:
1. Simple Equation: 1.23 ÷ x = a (where 'a' is a constant)
To solve for 'x', we need to isolate 'x' on one side of the equation.
-
Step 1: Multiply both sides by 'x'. This eliminates 'x' from the denominator on the left side.
(1.23 ÷ x) * x = a * x
1.23 = a * x
-
Step 2: Divide both sides by 'a'. This isolates 'x'.
1.23 ÷ a = (a * x) ÷ a
1.23 ÷ a = x
Therefore, x = 1.23 ÷ a
Example: 1.23 ÷ x = 3
x = 1.23 ÷ 3
x = 0.41
2. Equation with Additional Terms: 1.23 ÷ x + b = c (where 'b' and 'c' are constants)
To solve for 'x', we still need to isolate 'x', but we have an extra term to deal with.
-
Step 1: Subtract 'b' from both sides. This isolates the term containing 'x'.
(1.23 ÷ x + b) - b = c - b
1.23 ÷ x = c - b
-
Step 2: Let d = c - b. Now we have 1.23 ÷ x = d
-
Step 3: Multiply both sides by 'x'.
(1.23 ÷ x) * x = d * x
1.23 = d * x
-
Step 4: Divide both sides by 'd'.
1.23 ÷ d = (d * x) ÷ d
1.23 ÷ d = x
Therefore, x = 1.23 ÷ d = 1.23 ÷ (c - b)
Example: 1.23 ÷ x + 2 = 5
x = 1.23 ÷ (5 - 2)
x = 1.23 ÷ 3
x = 0.41
3. Equation with x on Both Sides: 1.23 ÷ x = x + e (where 'e' is a constant)
This type of equation is a bit more complex and may require the quadratic formula.
-
Step 1: Multiply both sides by 'x'.
(1.23 ÷ x) * x = (x + e) * x
1.23 = x² + ex
-
Step 2: Rearrange the equation into a quadratic form: ax² + bx + c = 0
x² + ex - 1.23 = 0
-
Step 3: Apply the quadratic formula:
x = (-b ± √(b² - 4ac)) / 2a
In this case, a = 1, b = e, and c = -1.23
x = (-e ± √(e² - 4 * 1 * -1.23)) / 2 * 1
x = (-e ± √(e² + 4.92)) / 2
-
Step 4: Solve for x using the two possible solutions from the ± sign. This will likely result in two different values for x.
Example: 1.23 ÷ x = x + 1
x² + x - 1.23 = 0
x = (-1 ± √(1² + 4.92)) / 2
x = (-1 ± √(5.92)) / 2
x = (-1 ± 2.433) / 2
x₁ = (-1 + 2.433) / 2 = 1.433 / 2 = 0.7165
x₂ = (-1 - 2.433) / 2 = -3.433 / 2 = -1.7165
Therefore, x ≈ 0.7165 or x ≈ -1.7165
Practical Applications of 1.23 ÷ x
While the expression 1.23 ÷ x might seem abstract, it can represent various real-world scenarios:
- Sharing: Imagine you have 1.23 kg of candy and want to divide it equally among 'x' number of friends. The expression 1.23 ÷ x represents the amount of candy each friend receives.
- Rate Problems: If you travel 1.23 kilometers in 'x' hours, the expression 1.23 ÷ x represents your average speed in kilometers per hour.
- Scaling Recipes: Suppose a recipe calls for 1.23 cups of flour and serves 'x' people. The expression shows the flour needed per person. If you need to adjust the recipe for a different number of servings, you'll need to solve for 'x'.
- Financial Calculations: Imagine you have a fixed budget of $1.23 to spend on 'x' items. Then 1.23 ÷ x is the maximum you can spend on each item.
Common Mistakes and Pitfalls
Working with division and variables can lead to several common errors. Being aware of these mistakes can help you avoid them:
- Dividing by Zero: As mentioned earlier, dividing by zero is undefined. Always check if your solution for 'x' could result in division by zero in the original equation.
- Incorrect Order of Operations: Remember the order of operations (PEMDAS/BODMAS). Make sure to perform operations in the correct sequence.
- Sign Errors: Pay close attention to the signs (positive or negative) when working with negative values of 'x' or when solving equations.
- Algebraic Manipulation Errors: Double-check your algebraic steps when isolating 'x'. Ensure you are performing the same operation on both sides of the equation.
- Forgetting the Quadratic Formula: When dealing with equations where 'x' appears in both the numerator and denominator, rearranging the equation may lead to a quadratic equation. Remember to use the quadratic formula to solve for 'x'.
- Not Checking Your Answers: After solving for 'x', substitute your solution back into the original equation to verify that it is correct. This helps catch any errors made during the solving process.
Advanced Concepts and Further Exploration
The expression 1.23 ÷ x can be a stepping stone to more advanced mathematical concepts:
- Functions: The expression can be represented as a function, f(x) = 1.23/x. This allows you to analyze the behavior of the expression as 'x' changes. For example, you can graph the function to visualize its relationship.
- Limits: In calculus, you can explore the limit of the function as 'x' approaches infinity or zero. This helps understand the behavior of the expression at extreme values of 'x'.
- Rational Functions: 1.23/x is a simple example of a rational function, which is a function that can be expressed as the ratio of two polynomials. Understanding rational functions is crucial in advanced algebra and calculus.
- Inverse Proportionality: The relationship between 1.23 ÷ x and 'x' demonstrates inverse proportionality. This means that as 'x' increases, the value of the expression decreases proportionally. Inverse proportionality is a fundamental concept in physics and engineering.
Strategies for Mastering Division with Variables
Here are some effective strategies for improving your understanding and skills in working with expressions like 1.23 ÷ x:
- Practice Regularly: The more you practice, the more comfortable you will become with algebraic manipulation and solving equations.
- Work Through Examples: Study worked-out examples carefully to understand the steps involved in solving different types of problems.
- Use Online Resources: Many websites and apps offer practice problems and tutorials on algebra and equation solving.
- Seek Help When Needed: Don't hesitate to ask your teacher, tutor, or classmates for help if you are struggling with a particular concept.
- Break Down Complex Problems: If you encounter a complex equation, break it down into smaller, more manageable steps.
- Check Your Work: Always double-check your answers to ensure accuracy.
- Visualize the Concepts: Try to visualize the mathematical concepts to gain a deeper understanding. For example, think about how the value of 1.23 ÷ x changes as 'x' gets larger or smaller.
- Connect to Real-World Applications: Look for real-world examples of how expressions like 1.23 ÷ x are used. This can make the concepts more relatable and easier to understand.
The Importance of a Solid Foundation
Mastering basic algebraic concepts like division with variables is essential for success in more advanced mathematics and science courses. A solid foundation in these fundamental skills will enable you to tackle more complex problems with confidence. Don't underestimate the importance of understanding the basics! Taking the time to master these concepts will pay off in the long run.
Conclusion: Embracing the Power of Division
The seemingly simple expression 1.23 ÷ x unveils the power and versatility of division in algebra. Understanding how to manipulate and solve equations involving this expression is a crucial skill for anyone pursuing mathematics, science, or engineering. By understanding the fundamental principles, practicing regularly, and avoiding common pitfalls, you can master this skill and unlock a deeper understanding of the world around you. So, embrace the power of division and continue your journey of mathematical exploration!
Latest Posts
Latest Posts
-
Factors Affecting Reaction Rate Lab Answers
Nov 15, 2025
-
Citizen In The Community Merit Badge Workbook
Nov 15, 2025
-
Which Accurately Describes The Supremacy Clause
Nov 15, 2025
-
So Foul And Fair A Day I Have Not Seen
Nov 15, 2025
-
Demand Is Said To Be Inelastic If
Nov 15, 2025
Related Post
Thank you for visiting our website which covers about 1.23 1 Lab Divide By X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.